Tutorial

You will solve the following problem using a computer to do some of the more tedious calculations.

Problem

Anna is investigating the relationship between exercise and resting heart rate. She takes a of 19 people in her year group and records for each person

• their resting heart rate, \(h\) beats per minute.

• the number of minutes, \(m\), spent exercising each week.

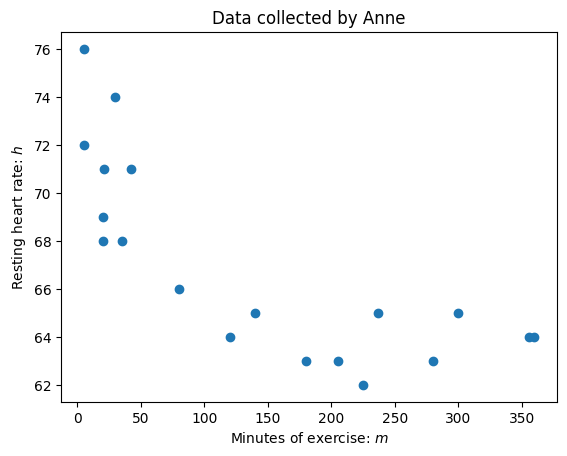
A table with the data is here:

Table 1 Collected data from Anna’s year group.

h	m
76.0	5
72.0	5
71.0	21
74.0	30
71.0	42
69.0	20
68.0	20
68.0	35
66	80.0
64	120.0
65	140.0
63	180.0
63	205.0
62	225.0
65	237.0
63	280.0
65	300.0
64	356.0
64	360.0

You can see a scatter plot below.

1. For all collected values of \(h\) and \(m\) obtain:

   • The mean

   • The median

   • The quartiles

   • The standard deviation

   • The variation

   • The maximum

   • The minimum

2. Obtain the Pearson Coefficient of correlation for the variables \(h\) and \(m\).

3. Obtain the line of best fit for variables \(x\) and \(y\) as defined by: $\(\begin{split}x=\ln(m)\qquad y=\ln(h)\end{split}\)$

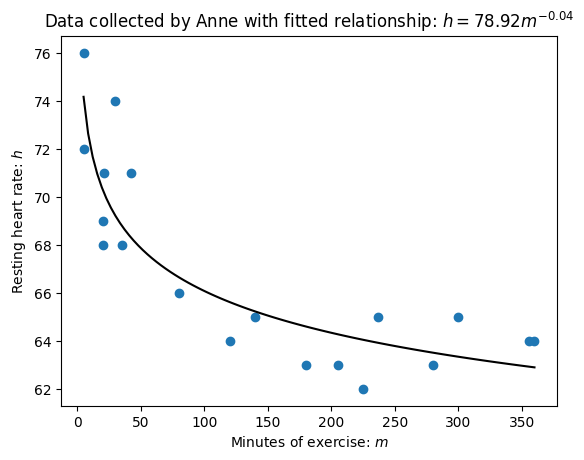
4. Using the above obtain a relationship between \(m\) and \(h\) of the form: $\(\begin{split}h=cm^k\end{split}\)$

Start by inputting all the data:

h = (
    76.0,
    72.0,
    71.0,
    74.0,
    71.0,
    69.0,
    68.0,
    68.0,
    66.0,
    64.0,
    65.0,
    63.0,
    63.0,
    62.0,
    65.0,
    63.0,
    65.0,
    64.0,
    64.0,
)
m = (
    5,
    5,
    21,
    30,
    42,
    20,
    20,
    35,
    80,
    120,
    140,
    180,
    205,
    225,
    237,
    280,
    300,
    356,
    360,
)

The main tool you are going to use for this is statistics.

import statistics as st

To calculate the mean:

st.mean(h)

67.0

st.mean(m)

140.05263157894737

To calculate the median:

st.median(h)

65.0

st.median(m)

120

To calculate the quartiles, use statistics.quantiles and specify that you want to separate the date in to \(n=4\) quarters.

st.quantiles(h, n=4)

[64.0, 65.0, 71.0]

st.quantiles(m, n=4)

[21.0, 120.0, 237.0]

Note that this calculation confirms the median which corresponds to the 50% quartile. To calculate the sample standard deviation:

st.stdev(h)

4.123105625617661

st.stdev(m)

124.46662813970593

To calculate the sample variance:

st.variance(h)

17.0

st.variance(m)

15491.941520467837

To compute that maximum:

max(h)

76.0

max(m)

360

To compute the minimum:

min(h)

62.0

min(m)

5

In order to compute the Pearson Coefficient of correlation use statistics.correlation:

st.correlation(h, m)

-0.7686142969026402

This negative value indicates a negative correlation between \(h\) and \(m\), indicating that the more you exercise the lower your heart rate is likely to be.

To calculate the line of best fit for the transformed variables we need to first create them. We will do this using a list comprehension. As you are doing everything numerically, we will use math.log which by default computes the natural logarithm:

import math
x = [math.log(value) for value in m]
y = [math.log(value) for value in h]

Now to compute the line of best fit use statistics.linear_regression:

slope, intercept = st.linear_regression(x, y)

The slope is:

slope

-0.03854770754231997

The intercept is:

intercept

4.368415819445762

Recall the transformation of the variables:

\[x=\ln(m)\qquad y=\ln(h)\]

You now have the relationship:

\[y=ax + b\]

Where \(a\) corresponds to the slope and \(b\) corresponds to the intercept.

The question asks for a relationship between \(m\) and \(h\) of the form:

\[h=cm^k\]

You can use sympy to manipulate the expressions:

import sympy as sym

h = sym.Symbol("h")
m = sym.Symbol("m")
a = sym.Symbol("a")
b = sym.Symbol("b")
x = sym.ln(m)
y = sym.ln(h)

A general line of best fit for \(x\) and \(y\) can be expressed in terms of \(m\) and \(h\):

line = sym.Eq(lhs=y, rhs=a * x + b)
line

\[\displaystyle \log{\left(h \right)} = a \log{\left(m \right)} + b\]

Taking the exponential of both sides gives the required relationship:

sym.exp(line.lhs)

\[\displaystyle h\]

sym.expand(sym.exp(line.rhs))

\[\displaystyle e^{b} e^{a \log{\left(m \right)}}\]

Which can be rewritten as:

\[ e^bm^a \]

Substituting our values for the slope and intercept in to these expressions gives the required relationship:

sym.exp(line.rhs).subs({a: slope, b: intercept})

\[\displaystyle \frac{78.9185114479915}{m^{0.03854770754232}}\]

Below is a plot that shows this relationship:

Important

In this tutorial you have

• Calulated values of central tendency and spread;

• Calculated some bivariate coefficient;

• Fitted a line of best fit.