How#

Calculate measures of spread and tendency#

Calculate a mean#

We can calculate the mean of a set of data using statistics.mean which takes an iterable.

Tip

statistics.mean(data)

For example to calculate the mean of \((1, 5, 10, 12, 13, 20)\):

import statistics as st

data = (1, 5, 10, 12, 13, 20)
st.mean(data)

10.166666666666666

Calculate a median#

We can calculate the median of a set of data using statistics.median which takes an iterable.

Tip

statistics.median(data)

For example to calculate the median of \((1, 5, 10, 12, 13, 20)\):

import statistics as st

data = (1, 5, 10, 12, 13, 20)
st.median(data)

11.0

Calculate the population standard deviation#

We can calculate the population standard deviation of a set of data using statistics.pstdev which takes an iterable.

Tip

statistics.pstdev(data)

For example to calculate the population standard deviation of \((1, 5, 10, 12, 13, 20)\):

import statistics as st

data = (1, 5, 10, 12, 13, 20)
st.pstdev(data)

6.039223643997813

Calculate the sample standard deviation#

We can calculate the sample standard deviation of a set of data using statistics.stdev which takes an iterable.

Tip

statistics.stdev(data)

For example to calculate the sample standard deviation of \((1, 5, 10, 12, 13, 20)\):

import statistics as st

data = (1, 5, 10, 12, 13, 20)
st.stdev(data)

6.6156380392723015

Calculate the population variance#

We can calculate the population variance of a set of data using statistics.pvariance which takes an iterable.

Tip

statistics.pvariance(data)

For example to calculate the population variance of \((1, 5, 10, 12, 13, 20)\):

import statistics as st

data = (1, 5, 10, 12, 13, 20)
st.pvariance(data)

36.47222222222222

Calculate the sample variance#

We can calculate the sample variance of a set of data using statistics.variance which takes an iterable.

Tip

statistics.variance(data)

For example to calculate the sample variance of \((1, 5, 10, 12, 13, 20)\):

import statistics as st

data = (1, 5, 10, 12, 13, 20)
st.variance(data)

43.766666666666666

Calculate the maximum#

We can calculate the maximum of a set of data use max which takes an iterable:

Tip

max(data)

For example to calculate the maximum of \((1, 5, 10, 12, 13, 20)\):

data = (1, 5, 10, 12, 13, 20)
max(data)

20

Calculate the minimum#

We can calculate the minimum of a set of data use max which takes an iterable:

Tip

min(data)

For example to calculate the minimum of \((1, 5, 10, 12, 13, 20)\):

data = (1, 5, 10, 12, 13, 20)
min(data)

1

Calculate quantiles#

To calculate cut points dividing data in to \(n\) intervals of equal probability we can use statistics.quantiles which takes an iterable and a number of intervals.

Tip

statistics.quantiles(data, n)

For example to calculate the cut points that divide \((1, 5, 10, 12, 13, 20)\) in to 4 intervals of equal probability (in this case the quantiles are called quartiles):

import statistics as st

data = (1, 5, 10, 12, 13, 20)
st.quantiles(data, n=4)

[4.0, 11.0, 14.75]

Calculate the sample covariance#

To calculate the sample covariance of two data sets we can use statistics.covariance which takes two iterables.

Tip

statistics.covariance(first_data_set, second_data_set)

For example to calculate the sample covariance of \(x=(1, 5, 10, 12, 13, 20)\) and \(y=(3, -3, 6, -2, 1, 2)\):

import statistics as st

x = (1, 5, 10, 12, 13, 20)
y = (3, -3, 6, -2, 1, 2)
st.covariance(x, y)

1.1666666666666674

Calculate the Pearson correlation coefficient#

To calculate the correlation coefficient of two data sets we can use statistics.correlation which takes two iterables.

Tip

statistics.correlation(first_data_set, second_data_set)

For example to calculate the correlation coefficient of \(x=(1, 5, 10, 12, 13, 20)\) and \(y=(3, -3, 6, -2, 1, 2)\):

import statistics as st

x = (1, 5, 10, 12, 13, 20)
y = (3, -3, 6, -2, 1, 2)
st.correlation(x, y)

0.05325222181462787

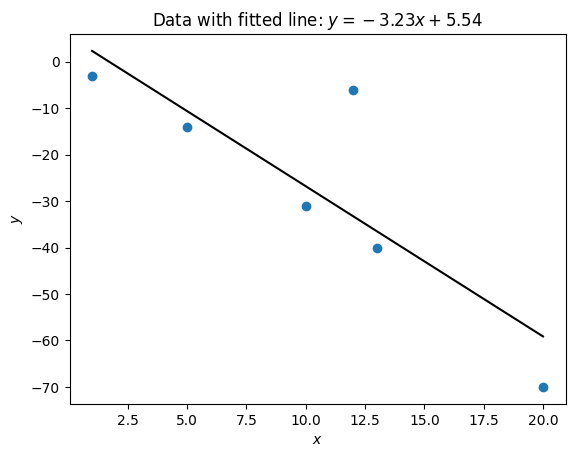
Fit a line of best fit#

To carry out linear regression to fit a line of best fit between two data sets we can use statistics.linear_regression which takes two iterables and returns a tuple with the slope and the intercept of the line.

Tip

statistics.linear_regression(first_data_set, second_data_set)

For example to calculate the correlation coefficient of \(x=(1, 5, 10, 12, 13, 20)\) and \(y=(-3, -14, -31, -6, -40, -70)\):

import statistics as st

x = (1, 5, 10, 12, 13, 20)
y = (-3, -14, -31, -6, -40, -70)
st.linear_regression(x, y)

LinearRegression(slope=-3.2338156892612333, intercept=5.543792840822537)
../../../_images/main_24_0.png

How to create an instance of the normal distribution#

A normal distribution with mean \(\mu\) and standard deviation \(\sigma\) can be created using statistics.NormalDist:

Tip

statistics.NormalDist(mu, sigma)

For example to create the normal distribution with \(\mu=3\) and \(\sigma=.5\):

import statistics as st

distribution = st.NormalDist(mu=3, sigma=.5)
distribution

NormalDist(mu=3.0, sigma=0.5)

How to use the cumulative distribution function of a normal distribution#

For an instance of a normal distribution with mean \(\mu\) and \(\sigma\), the cumulative distribution function which gives \(F(x)=P(X<x)\) (the probability that the normally distributed random variable is less than \(X\)) can be accessed using statistics.NormaDist.cdf.

Tip

distribution = statistics.NormalDist(mu, sigma)
distribution.cdf(x)

For example to find the probability that \(X<2\) for a normally distributed random variable with \(\mu=3\) and \(\sigma=.5\):

import statistics as st

distribution = st.NormalDist(mu=3, sigma=.5)
distribution.cdf(2)

0.02275013194817921

How to use the inverse cumulative distribution function of a normal distribution#

For an instance of a normal distribution with mean \(\mu\) and \(\sigma\), the inverse cumulative distribution function which for a given \(p\) gives \(x\) such that \(p=P(X<x)\) can be accessed using statistics.NormaDist.inv_cdf.

Tip

distribution = statistics.NormalDist(mu, sigma)
distribution.inv_cdf(p)

For example to find the value of \(X\) for which a normally distributed random variable with \(\mu=3\) and \(\sigma=.5\) will be less than with probability \(.7\).

import statistics as st

distribution = st.NormalDist(mu=3, sigma=.5)
distribution.inv_cdf(.7)

3.2622002563540202