Motivating Example: Coffee clubs and the common good game¶
Across a large university campus, students form informal coffee clubs. Each day, students join clubs to share a cafetière of coffee and discuss algebraic topology or the latest student gossip. There are three types of students:
Cooperators always bring a scoop of ground coffee to the club.
Defectors show up empty-handed but still drink the coffee.
Loners prefer to skip clubs and enjoy a quiet cup alone — reliable, if a bit less exciting.
In each club, all coffee brought is pooled, brewed, and the resulting pot is shared equally among the attendees. If there are cooperators, the pot yields units of value to be divided among all participants (cooperators and defectors). The loners, who don’t attend clubs, receive a fixed payoff .
Let the total population be normalized to 1, with:
the proportion of cooperators,
the proportion of defectors,
the proportion of loners.
Assuming the population is large and well-mixed, we can model the average payoff to each strategy as:
Here, is the return factor of the public good (coffee), and the subtraction of 1 from reflects the cost of bringing coffee.
These payoffs are used in the replicator dynamics equation, which models how the frequency of each strategy changes over time:
where is the population average payoff.
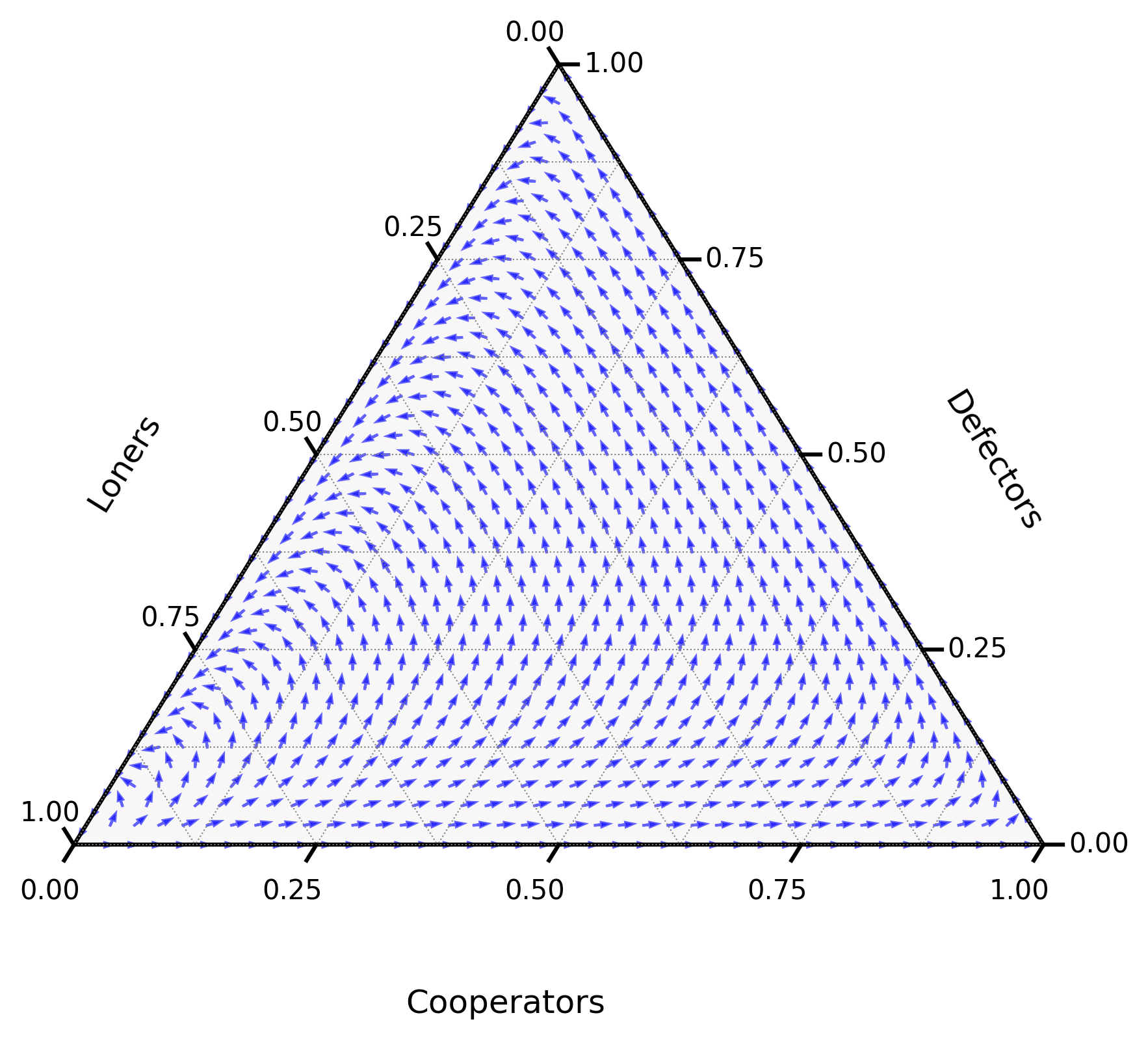
Figure 1:A diagram showing the direction of the derivative as given by (1) for and .
Strategies that do better than the average will increase in frequency; those that do worse will decline. This feedback mechanism drives the evolution of behavior in the population — capturing the shifting fortunes of cooperators, defectors, and loners on campus.
As we will see, this system often exhibits cyclical behavior: when most students cooperate, defectors thrive; when defection becomes too common, students prefer to be loners; when clubs are small and rare, cooperation becomes appealing again. These cycles — and their stability — are precisely what replicator dynamics helps us understand.
Theory¶
Definition: Replicator Dynamics Equation¶
Consider a population with types of individuals. Let denote the proportion of individuals of type , so that .
Suppose the fitness of an individual of type depends on the state of the entire population, through a population-dependent fitness function .
The replicator dynamics equation is given by:
where the average population fitness is defined as:
This equation describes the change in frequency of each type as proportional to how much better (or worse) its fitness is compared to the population average.
Example: The common good game¶
In the common good game around coffee clubs the replicator dynamics equation can be written as:
where:
Definition: Stable Population¶
For a given population game with types of individuals and fitness functions a stable population is one for which for all .
For a stable population :
so either: or .
Example: No interior point stable population in the common goods game¶
For the common good game around coffee clubs we have some immediate stable populations:
: indeed so that and so .
: indeed so that and so .
: indeed so that and so .
A question remains, is there a point in the interior of the simplex of Figure 1 that is stable? Such a point has , and which implies:
This is not possible as: for all .
Definition: Fitness of a strategy in a population¶
In a population with types let denote the fitness of an individual playing strategy in a population :
Example: A new student in the Common Goods Game¶
For the common good game if we consider a stable population where everyone is defecting and assume that a new student enters planning to cooperate 50% of the time and defect 50% of the time, their fitness is given by:
Definition: Post Entry Population¶
For a population with types of individuals Given a population (with ), some and a strategy (with ), the post entry population is given by:
Example: Post Entry Population for the Common Goods Game¶
For the common good game if we consider the stable population where everyone is defecting and assume that a new student enters the population planning to cooperate with a coffee club 50% of the time and defect 50% of the time the post entry population will be:
What is of interest in the field of evolutionary game theory is what happens to the post entry population: does this new student change the stability of the system or is the system going to go back to all students defecting?
Definition: Evolutionary Stable Strategy¶
A strategy is an evolutionarily stable strategy if for all sufficiently close to :
In practice sufficiently close implies that there exists some such that for all and for all the post entry population satisfies (12).
Example: Are Loners Evolutionarily Stable in the Common Goods Game¶
For the common good game we have seen that a population where everyone is a longer is stable. Let us check if it is evolutionarily stable.
We have:
Now to calculate the right hand side of (12):
which is strictly less than unless which it cannot as .
Definition: Pairwise Interaction Game¶
Given a population of types of individuals and a payoff matrix a pairwise interaction game is a game where the fitness is is given by:
This corresponds to a population where all individuals interact with all other individuals in the population and obtain a fitness given by the matrix .
Note that there is a linear algebraic equivalent to (15):
and then:
Example: The Hawk Dove Game¶
Consider a population of animals. These animals, when they interact, will always share their food. Due to a genetic mutation, some of these animals may act in an aggressive manner and not share their food. If two aggressive animals meet, they both compete and end up with no food. If an aggressive animal meets a sharing one, the aggressive one will take most of the food.
These interactions can be represented using the matrix :
In this scenario: what is the likely long-term effect of the genetic mutation?
Over time will:
The population resist the mutation and all the animals continue to share their food.
The population get taken over by the mutation and all animals become aggressive.
A mix of animals are present in the population: some act aggressively and some share.
To answer this question, we will model it as a pairwise interaction game with representing the population distribution. In this case:
represents the proportion of the population that shares.
represents the proportion of the population that acts aggressively.
In this case, the replicator dynamics equation becomes:
Note that so for simplicity of notation we will only use to represent the proportion of the population that shares.
Thus we can write the single differential equation:
We see that there are 3 stable populations:
: No sharers
: Only sharers
: A mix of both sharers and aggressive individuals.
This differential equation can then be solved numerically, for example using Euler’s Method to show the evolution of
Let us do this with a step size and an initial population of :
Recall, we use the update rule:
to give Table 1.
Table 1:Step by step application of Euler’s method to the Hawk Dove game with step size and .
| 0 | 0.0 | 0.600 | -0.048 | 0.595 |
| 1 | 0.1 | 0.595 | -0.046 | 0.591 |
| 2 | 0.2 | 0.591 | -0.044 | 0.586 |
| 3 | 0.3 | 0.586 | -0.042 | 0.582 |
| 4 | 0.4 | 0.582 | -0.040 | 0.578 |
| 5 | 0.5 | 0.578 | -0.038 | 0.574 |
| 6 | 0.6 | 0.574 | -0.036 | 0.571 |
| 7 | 0.7 | 0.571 | -0.035 | 0.567 |
| 8 | 0.8 | 0.567 | -0.033 | 0.564 |
| 9 | 0.9 | 0.564 | -0.031 | 0.561 |
| 10 | 1.0 | 0.561 | -0.030 | 0.558 |
If we repeat this with we obtain Table 2.
Table 2:Step by step application of Euler’s method to the Hawk Dove game with step size and .
| 0 | 0.0 | 0.400 | 0.048 | 0.405 |
| 1 | 0.1 | 0.405 | 0.046 | 0.409 |
| 2 | 0.2 | 0.409 | 0.044 | 0.414 |
| 3 | 0.3 | 0.414 | 0.042 | 0.418 |
| 4 | 0.4 | 0.418 | 0.040 | 0.422 |
| 5 | 0.5 | 0.422 | 0.038 | 0.426 |
| 6 | 0.6 | 0.426 | 0.036 | 0.429 |
| 7 | 0.7 | 0.429 | 0.035 | 0.433 |
| 8 | 0.8 | 0.433 | 0.033 | 0.436 |
| 9 | 0.9 | 0.436 | 0.031 | 0.439 |
| 10 | 1.0 | 0.439 | 0.030 | 0.442 |
It looks the population is converging to the population which has a mix of both sharers and aggressive types: . Figure 2 confirms this.
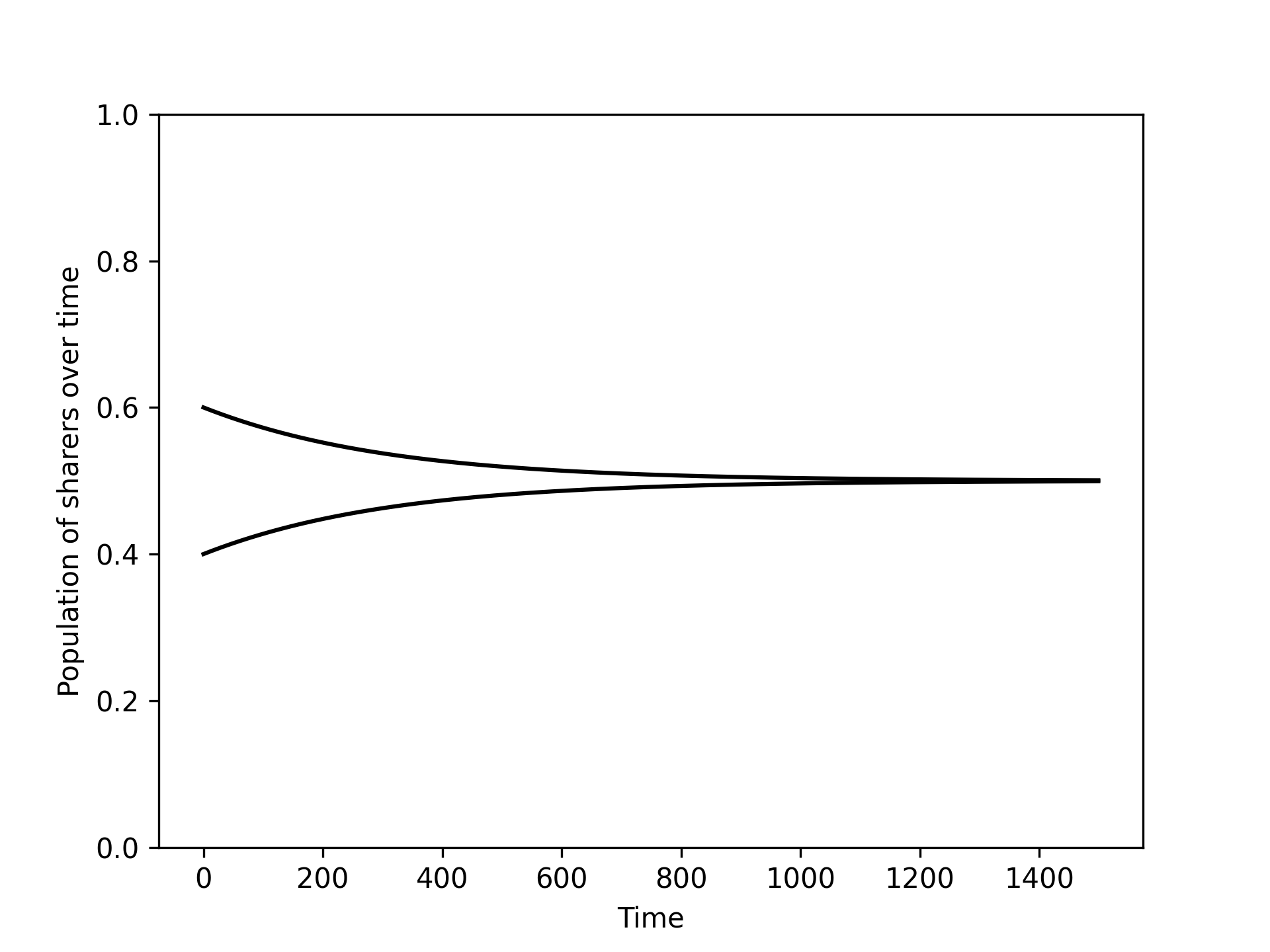
Figure 2:The numerical integration of the differential equation (21) with two different initial values of .
This indicates that is an evolutionary stable strategy. To confirm this we could repeat calculations using the definition of an evolutionary stable strategy however for pairwise interaction games there is a theoretic result that can be used instead.
Theorem: Characterisation of ESS in two-player games¶
Let be a strategy in a symmetric two-player game (so that ). Then is an evolutionarily stable strategy (ESS) if and only if, for all , one of the following conditions holds:
and
Conversely, if either of the above conditions holds for all , then is an ESS in the corresponding population game.
Proof¶
Assume is an ESS. Then, by definition, there exists such that for all and all , we have:
where is the mixed population state. Substituting into the expected fitness, we obtain:
Rearranging, this inequality holds for all sufficiently small if either:
(so the left-hand side is already greater); or
but , so the second-order term dominates as .
For the converse, suppose neither condition holds. Then either:
, so for small the inequality fails and is not stable, or
and , in which case the right-hand side is at least as large as the left for small , again contradicting stability.
Hence, the two conditions are necessary and sufficient for evolutionary stability.
This theorem gives us a practical method for identifying ESS:
Construct the associated symmetric two-player game.
Identify all symmetric Nash equilibria of the game.
For each symmetric Nash equilibrium, test the two conditions above.
Note that the first condition is very close to the condition for a strict Nash equilibrium, while the second adds a refinement that removes certain non-strict symmetric equilibria. This distinction is especially important when considering equilibria in strategies.
Example: Evolutionary stability in the Hawk-Dove game¶
Let us consider the Hawk-Dove game. The associated symmetric two-player game can be written in a general form. Let denote the value of the resource and the cost of conflict with .
Row player’s payoff matrix:
Column player’s payoff matrix:
To find symmetric Nash equilibria, we apply the support enumeration algorithm:
This gives
where individuals are aggressive with probability and share otherwise.
To determine whether this strategy is evolutionarily stable, we check the conditions of the characterisation theorem.
Crucially, because , the first condition does not hold. We must therefore verify the second condition:
Let be an arbitrary strategy. Then:
Subtracting the two expressions gives:
This inequality is strictly satisfied for all , so the second condition holds and is an evolutionarily stable strategy.
Definition: Replicator Mutator Dynamics Equation¶
An extension of the replicator equation is to allow for mutation. In this setting, reproduction is imperfect: individuals of a given type can give rise to individuals of another type.
This process is represented by a matrix , where denotes the probability that an individual of type is produced by an individual of type .
In this case, the replicator dynamics equation can be modified to yield the replicator-mutation equation:
Example: The Replicator Mutator Dynamics Equation for the Hawk Dove Game¶
Let there be a 10% change that aggressive individuals will produce sharing ones in which case the matrix is given by:
Example: Recovering the Replicator Dynamics Equation from the Replicator Mutator Dynamics Equation¶
Show that when (the identity matrix of size ) then the replicator dynamics equation corresponds to the replicator dynamics equation.
The replicator-mutation equation is:
As :
This gives:
Definition: Asymmetric Replicator Dynamics Equation¶
A further extension of the replicator dynamics framework accounts for populations divided into two distinct subsets. Individuals in the first population are one of possible types, while those in the second population are one of possible types.
This setting arises naturally in asymmetric games, where the roles of the players differ and the strategy sets need not be the same (i.e., ). In such cases, the standard replicator equation does not apply directly.
The asymmetric replicator dynamics equations describe the evolution of strategy distributions and in each population:
Here:
and are the expected fitnesses of type and in each population respectively,
and denote the average fitnesses in the respective populations.
Example: Tennis Serve and Return¶
In tennis, serving and receiving form an asymmetric interaction. The server (row player) chooses one of two serves, while the receiver (column player) chooses one of three possible return strategies.
The server can deliver a power or spin serve. The receiver can either prepare for power, cover a wide spin, or take an early aggressive position.
This leads to an asymmetric game where the server has 2 strategies and the receiver has 3. The game matrices are:
These matrices are based on the following assumptions:
If the server uses a power serve () and the receiver prepares for it (), the server has some success (payoff 3), but the receiver also does reasonably well (payoff 1).
If the server tries spin () and the receiver is covering for it (), the payoff is more balanced (2 for each).
A mismatch, such as a power serve into a receiver expecting spin ( vs ), favors the server more (payoff 1 vs 3).
Conversely, if the receiver takes an early position and guesses right against spin ( vs ), they gain a big advantage (payoff 1 vs 4).
Let be the strategy distribution of the server and that of the receiver. The asymmetric replicator dynamics for this game are:
Figure 3 shows the numerical solutions of these differential equations over time.
Preparing for Power quickly dies out as a strategy;
There is a cycle with the server changing between power and spin while the returner cycles between preparing for spin and taking an aggressive position.
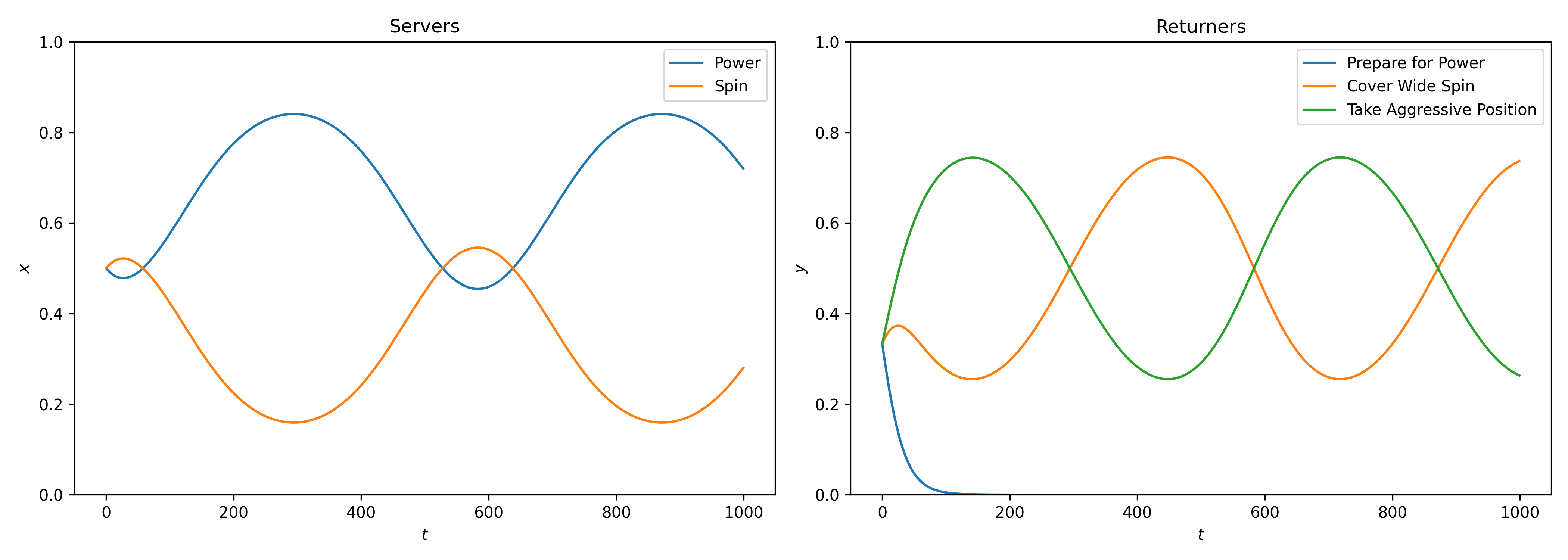
Figure 3:Numerical solutions to the asymmetric replicator dynamics equation. Preparing for power quickly dies out as a played strategy in the population. There is a cycle of the 2 remaining strategies for the returner and for the server although power remains the strategy player most often.
Exercises¶
Programming¶
In Appendix: Numerical Integration, we introduce general programming approaches for numerically solving differential equations. These apply directly to the replicator dynamics equation. Here, we focus on tools specifically tailored to pairwise interaction games.
Solving symmetric replicator dynamics¶
The Nashpy library provides built-in functionality for solving the replicator
dynamics equation in a
pairwise interaction game.
Let us consider the classic Rock–Paper–Scissors game:
import nashpy as nash
import numpy as np
M_r = np.array([[0, 1, -1], [-1, 0, 1], [1, -1, 0]])
game = nash.Game(M_r)We can compute the population trajectory from an initial distribution:
x0 = np.array([1 / 6, 1 / 6, 2 / 3])
timepoints = np.linspace(0, 10, 1500)
xs = game.replicator_dynamics(y0=x0, timepoints=timepoints).T
xsarray([[0.16666667, 0.16611198, 0.16555975, ..., 0.53953201, 0.53854678,
0.53755904],
[0.16666667, 0.16722383, 0.16778347, ..., 0.09354312, 0.09343612,
0.09333053],
[0.66666667, 0.66666419, 0.66665678, ..., 0.36692487, 0.36801711,
0.36911043]], shape=(3, 1500))To visualize the evolution of strategy frequencies over time:
import matplotlib.pyplot as plt
plt.figure()
plt.plot(xs.T)
plt.ylim(0, 1)
plt.legend(["$x_1$", "$x_2$", "$x_3$"])
plt.ylabel("Distribution")
plt.xlabel("Time")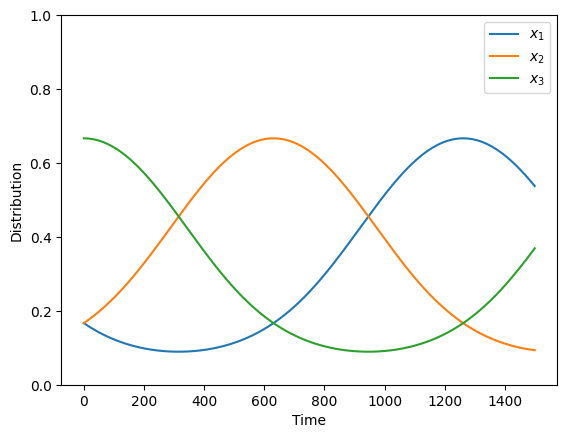
Plotting a simplex with ternary¶
The ternary library Harper, 2019 allows for plotting trajectories on a simplex, ideal for representing three-component distributions that sum to one.
We can use it to plot the Rock–Paper–Scissors trajectory:
import ternary
figure, tax = ternary.figure(scale=1.0)
tax.boundary()
tax.gridlines(multiple=0.2, color="black")
# Plot the data
tax.plot(xs.T, linewidth=2.0, label="$x$")
tax.ticks(axis='lbr', multiple=0.2, linewidth=1, tick_formats="%.1f")
tax.legend()
tax.left_axis_label("Scissors")
tax.right_axis_label("Paper")
tax.bottom_axis_label("Rock")
tax.ax.axis('off')
tax.show()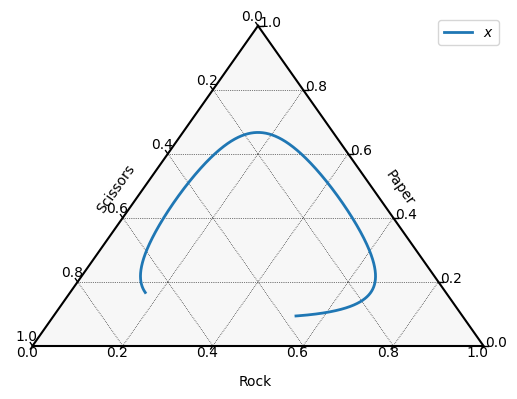
Solving Asymmetric Replicator dynamics¶
The Nashpy library also supports numerical solutions for the asymmetric replicator dynamics equation.
M_r = np.array([[3, 1, 2], [4, 2, 1]])
M_c = np.array([[1, 3, 2], [0, 2, 4]])
game = nash.Game(M_r, M_c)
x0 = np.array([1/2, 1/2])
y0 = np.array([1/3, 1/3, 1/3])
timepoints = np.linspace(0, 20, 1000)
xs, ys = game.asymmetric_replicator_dynamics(x0=x0, y0=y0, timepoints=timepoints)
xsarray([[0.5 , 0.5 ],
[0.49836507, 0.50163493],
[0.49679694, 0.50320306],
...,
[0.72372346, 0.27627654],
[0.7218324 , 0.2781676 ],
[0.7199282 , 0.2800718 ]], shape=(1000, 2))The corresponding trajectory for the column player’s strategy distribution:
ysarray([[ 3.33333333e-01, 3.33333333e-01, 3.33333333e-01],
[ 3.23391408e-01, 3.36602736e-01, 3.40005857e-01],
[ 3.13590591e-01, 3.39735869e-01, 3.46673540e-01],
...,
[-1.06554178e-13, 7.35381389e-01, 2.64618611e-01],
[-1.25688203e-13, 7.36036679e-01, 2.63963321e-01],
[-1.40730981e-13, 7.36668819e-01, 2.63331181e-01]],
shape=(1000, 3))Notable Research¶
The original conceptual idea of an evolutionarily stable strategy (ESS) was formulated by Maynard Smith Smith & Price, 1973Smith, 1982. Although these works did not explicitly introduce the replicator dynamics equation, they were foundational in connecting game theory with evolutionary biology.
The first formal presentation of the replicator dynamics equation appeared in Taylor & Jonker, 1978, which directly built upon Maynard Smith’s ESS framework. This formulation was later extended to multi-player games in Palm, 1984, and to asymmetric populations in Accinelli & Carrera, 2011.
Several influential applications of replicator dynamics have since emerged. For example, Komarova et al., 2001 used replicator-mutator dynamics to model the spread of grammatical structures in language populations. In the context of cooperation, Hilbe et al., 2013 applied the model to study the evolution of reactive strategies, while Knight et al., 2024 recently demonstrated how extortionate strategies fail to persist under evolutionary pressure.
A particularly notable extension is found in Weitz et al., 2016, where the game itself changes dynamically depending on the population state. This approach is especially relevant in modeling the tragedy of the commons and other environmental feedback systems.
In Lv et al., 2023, a model similar to the one in Section: Motivating Example is examined using both replicator dynamics and a discrete population model. The latter is explored in detail in Chapter: Moran Process. Remarkably, the replicator dynamics equation emerges as the infinite-population limit of the discrete model—a connection rigorously established in Traulsen et al., 2005.
Conclusion¶
The replicator dynamics equation provides a powerful lens through which to study strategy evolution in large populations. By linking the fitness of strategies to their growth or decline in the population, it captures the essence of selection and adaptation.
Throughout this chapter, we explored how replicator dynamics:
arise naturally in settings like public goods provision (e.g., coffee clubs),
describe population change in terms of differential equations,
connect with the concept of evolutionarily stable strategies (ESS),
extend to incorporate mutation and asymmetry,
and can be simulated and visualized with numerical methods and tools.
From modelling simple two-strategy contests to rich three-strategy dynamics on a simplex, replicator dynamics offer an interpretable and analytically rich framework for evolutionary game theory. Table Table 3 gives a summary of the main concepts of this chapter.
Table 3:Summary of key concepts in replicator dynamics.
| Concept | Description |
|---|---|
| Replicator Dynamics Equation | Models strategy frequency change based on relative fitness |
| Average Population Fitness () | Weighted average of individual fitnesses |
| Stable Population | A distribution where no strategy’s frequency changes over time |
| Evolutionarily Stable Strategy (ESS) | A stable strategy resistant to invasion by nearby alternatives |
| Post Entry Population | Perturbed population after a rare mutant enters |
| Replicator-Mutator Equation | Extension accounting for imperfect strategy transmission |
| Asymmetric Replicator Dynamics | Models evolution in multi-population or role-asymmetric settings |
| Pairwise Interaction Game | Fitness determined by payoffs in repeated pairwise interactions |
- Harper, M. (2019). python-ternary: Ternary Plots in Python. Zenodo 10.5281/Zenodo.594435. 10.5281/zenodo.594435
- Smith, J. M., & Price, G. R. (1973). The logic of animal conflict. Nature, 246(5427), 15–18.
- Smith, J. M. (1982). Evolution and the Theory of Games. In Did Darwin get it right? Essays on games, sex and evolution (pp. 202–215). Springer.
- Taylor, P. D., & Jonker, L. B. (1978). Evolutionary stable strategies and game dynamics. Mathematical Biosciences, 40(1–2), 145–156.
- Palm, G. (1984). Evolutionary stable strategies and game dynamics for n-person games. Journal of Mathematical Biology, 19, 329–334.
- Accinelli, E., & Carrera, E. J. S. (2011). Evolutionarily stable strategies and replicator dynamics in asymmetric two-population games. In Dynamics, Games and Science I: DYNA 2008, in Honor of Maurı́cio Peixoto and David Rand, University of Minho, Braga, Portugal, September 8-12, 2008 (pp. 25–35). Springer.
- Komarova, N. L., Niyogi, P., & Nowak, M. A. (2001). The evolutionary dynamics of grammar acquisition. Journal of Theoretical Biology, 209(1), 43–59.
- Hilbe, C., Nowak, M. A., & Sigmund, K. (2013). Evolution of extortion in iterated prisoner’s dilemma games. Proceedings of the National Academy of Sciences, 110(17), 6913–6918.
- Knight, V., Harper, M., Glynatsi, N. E., & Gillard, J. (2024). Recognising and evaluating the effectiveness of extortion in the Iterated Prisoner’s Dilemma. PloS One, 19(7), e0304641.
- Weitz, J. S., Eksin, C., Paarporn, K., Brown, S. P., & Ratcliff, W. C. (2016). An oscillating tragedy of the commons in replicator dynamics with game-environment feedback. Proceedings of the National Academy of Sciences, 113(47), E7518–E7525.
- Lv, S., Li, J., & Zhao, C. (2023). The evolution of cooperation in voluntary public goods game with shared-punishment. Chaos, Solitons & Fractals, 172, 113552.
- Traulsen, A., Claussen, J. C., & Hauert, C. (2005). Coevolutionary dynamics: from finite to infinite populations. Physical Review Letters, 95(23), 238701.