Motivating Example¶
We will motivate this chapter using a special case of Selten’s Chain Store Paradox Selten, 1978 which models an incumbent chain of stores that is well established and an entrant to the market.
Campus Caffeine, a mobile coffee van, is considering parking near a university where Latte Lords, a well-established bricks-and-mortar café, has been operating unchallenged. If Campus Caffeine enters, Latte Lords can slash prices for students (Fight) or maintain their premium pricing (Accommodate). If Campus Caffeine stays out, Latte Lords keeps enjoying high margins.
There are three outcomes which are shown as an extensive form game in Figure 1:
Campus Caffeine chooses to withdraw and does not enter the market: they receive a utility of 1 and Latte Lords continues to have a monopoly with which corresponds to a utility of 5.
Campus Caffeine enters the market and Latte Lords competes: this leads to low prices that give neither company a profit. They both obtain a utility of 0.
Campus Caffeine enters and Latte Lords accommodates: they both share the market obtaining a utility of 2.
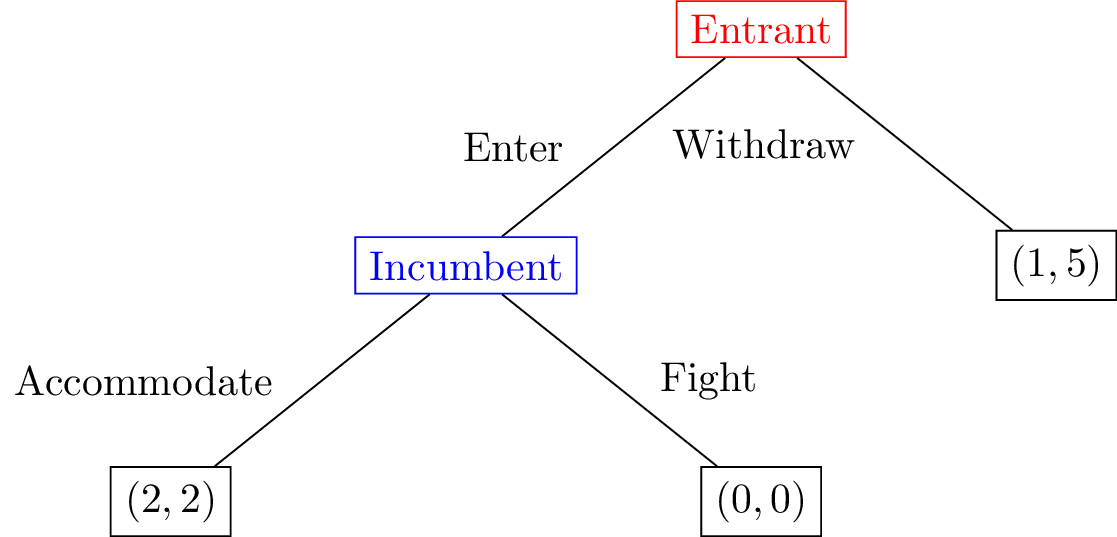
Figure 1:The extensive form game between Campus Caffeine and Latte Lords.
As described in Mapping Extensive Form Games to Normal Form it is possible to map an extensive form game to a normal form game. In this case we have:
giving:
The incumbent can threaten to fight the entrant however the entrant knows that this threat if carried out would be harmful to both of them. Thus the threat is in essence an empty threat: the entrant will enter and the incumbent will use their best response which is to accommodate.
This is an example of a degenerate game, the Nash equilibria was considered in Example: Support Enumeration for a degenerate game showing that there are in fact 3 of them:
: the entrant enters the market and the incumbent accommodates.
: the entrant withdraws and the incumbent fights.
: a mixture between the two.
This chapter will give the mathematical vocabulary to describe the difference between these equilibria.
Theory¶
To identify emergent behaviour in extensive form games we assume that players not only attempt to optimize their overall utility but optimize their utility conditional on any information set.
Definition: Sequential rationality¶
Sequential rationality: An optimal strategy for a player should maximise that player’s expected payoff, conditional on every information set at which that player has a decision.
With this notion in mind we can now define an analysis technique for extensive form games:
Definition: Backward induction¶
Backward induction: This is the process of analysing a game from back to front. At each information set we remove strategies that are dominated.
Example¶
Let us consider the game shown in Figure 2
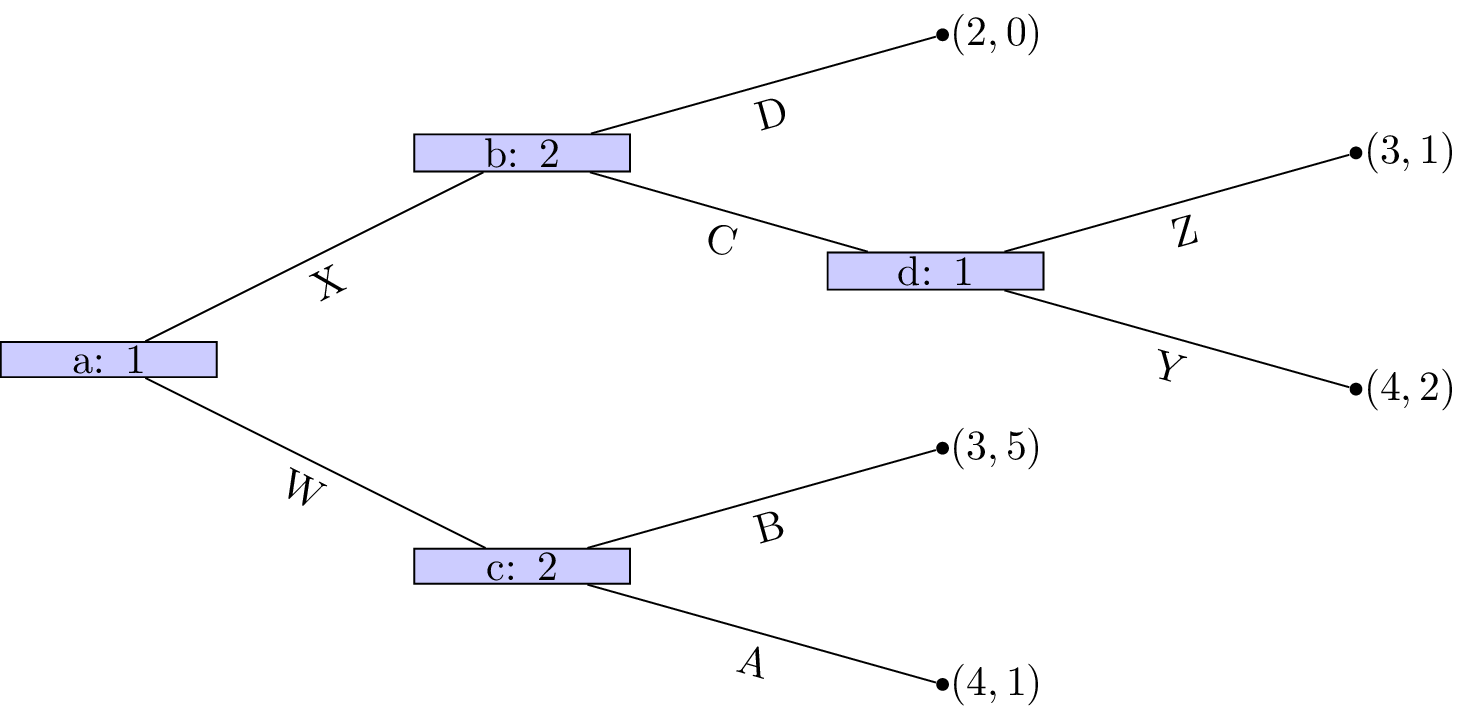
Figure 2:An extensive form game that we will use backwards induction on.
We see that at node that Z is a dominated action. So the game reduces as shown in Figure 3.
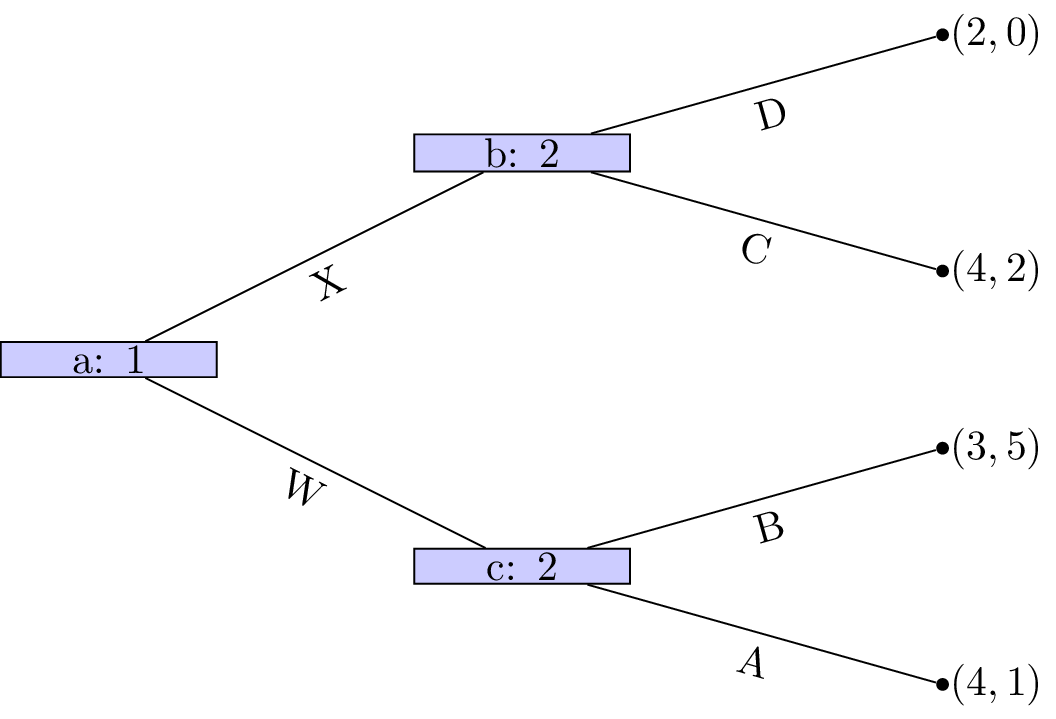
Figure 3:Reducing the game because Z is a dominated action.
Player 1s strategy profile is (Y). At node A is a dominated action so that the game reduces as shown in Figure 4.
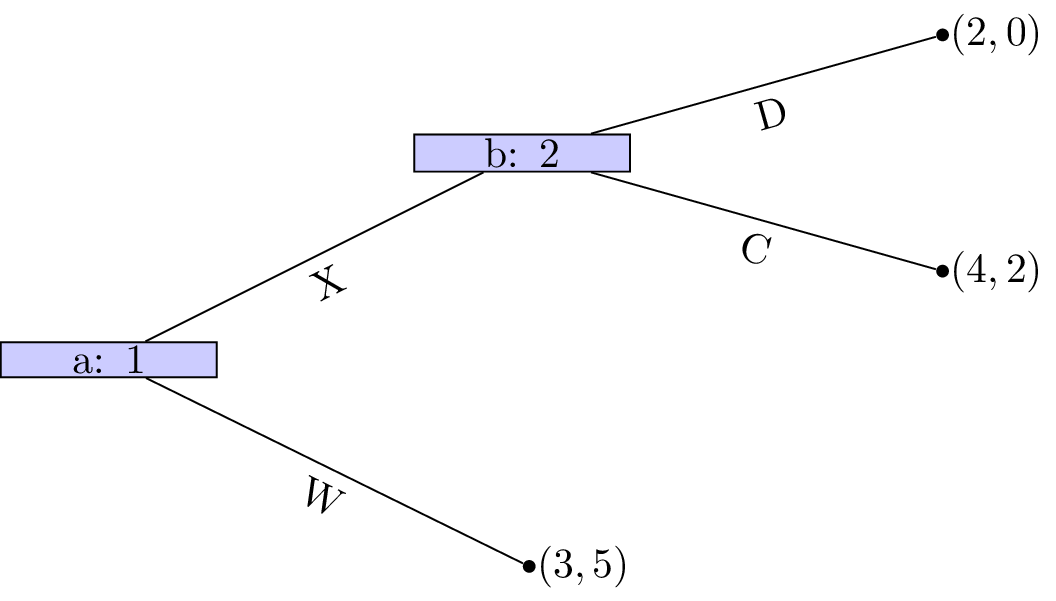
Figure 4:Reducing the game because A is a dominated action.
Player 2s strategy profile is (B). At node D is a dominated action so that the game reduces as shown.
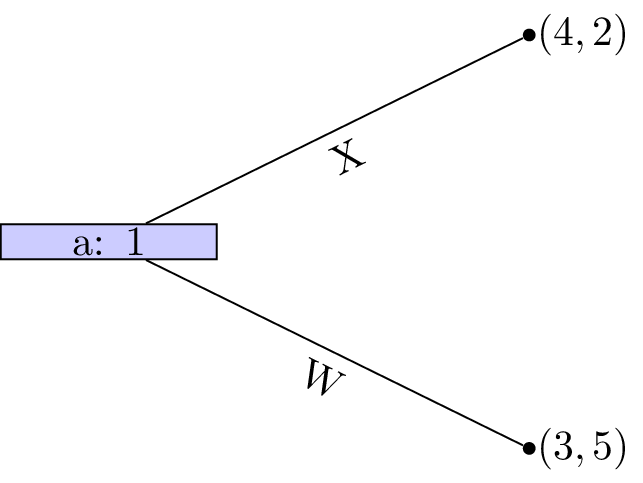
Figure 5:Reducing the game because D is a dominated action.
Player 2s strategy profile is thus (C,B) and finally strategy W is dominated for player 1 whose strategy profile is (X,Y). This pair of strategies form a Nash equilibrium.
Theorem of existence of Nash equilibrium in games of perfect information.¶
Every finite game with perfect information has a Nash equilibrium in pure strategies. Backward induction identifies an equilibrium.
Proof:
Recalling the properties of sequential rationality we see that no player will have an incentive to deviate from the strategy profile found through backward induction. Secondly every finite game with perfect information can be solved using backward inductions which gives the result.
Definition: Subgame¶
In an extensive form game, a node is said to initiate a subgame if and only if and all successors of are in information sets containing only successors of .
Example: a game where all nodes initiate subgames¶
A game where all nodes initiate a subgame is given in Figure 6.
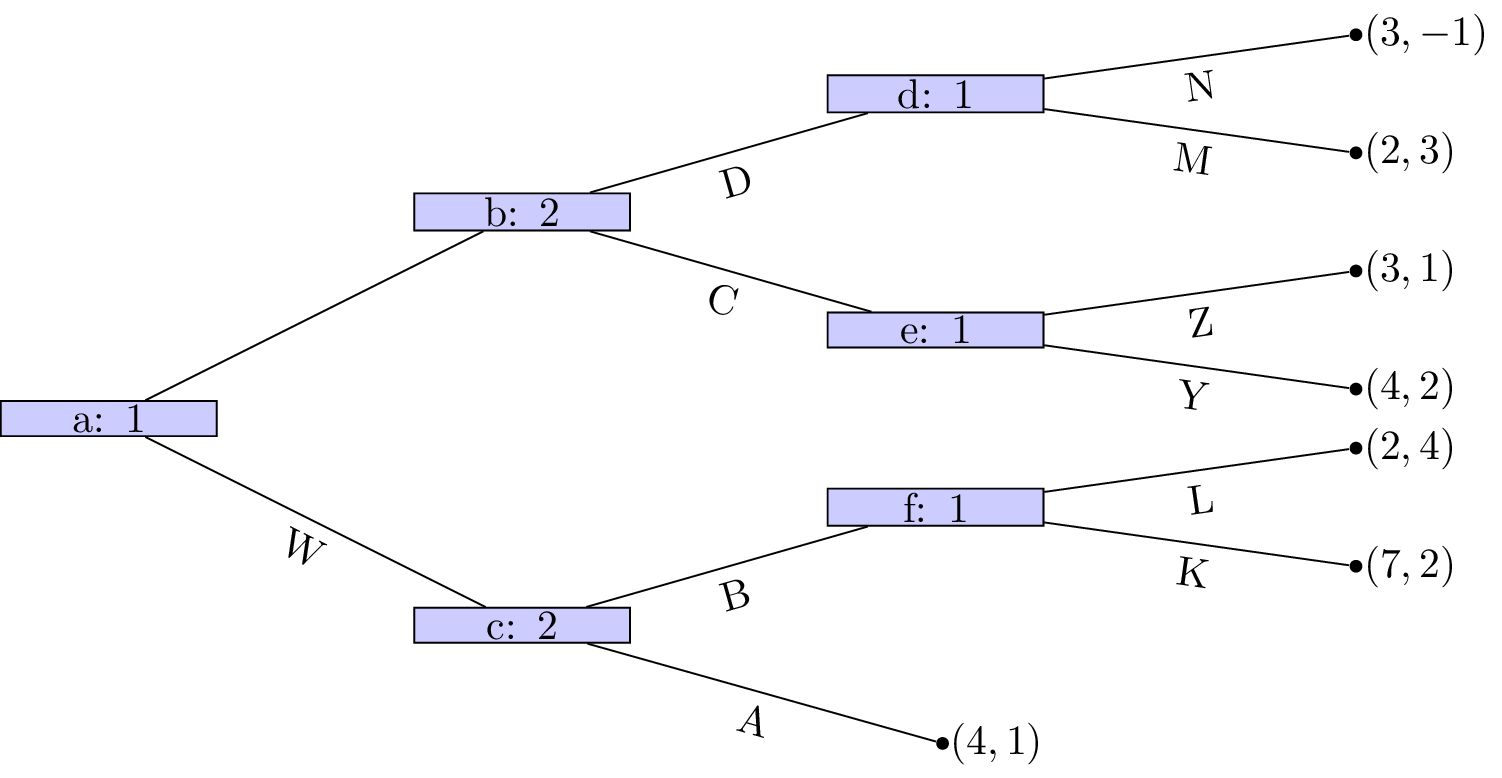
Figure 6:An extensive form game where all nodes initiate a subgame.
Example: a game where all nodes do not initiate subgames¶
A game that does not have perfect information nodes , and initiate subgames but all of ’s successors do not is shown in Figure 7
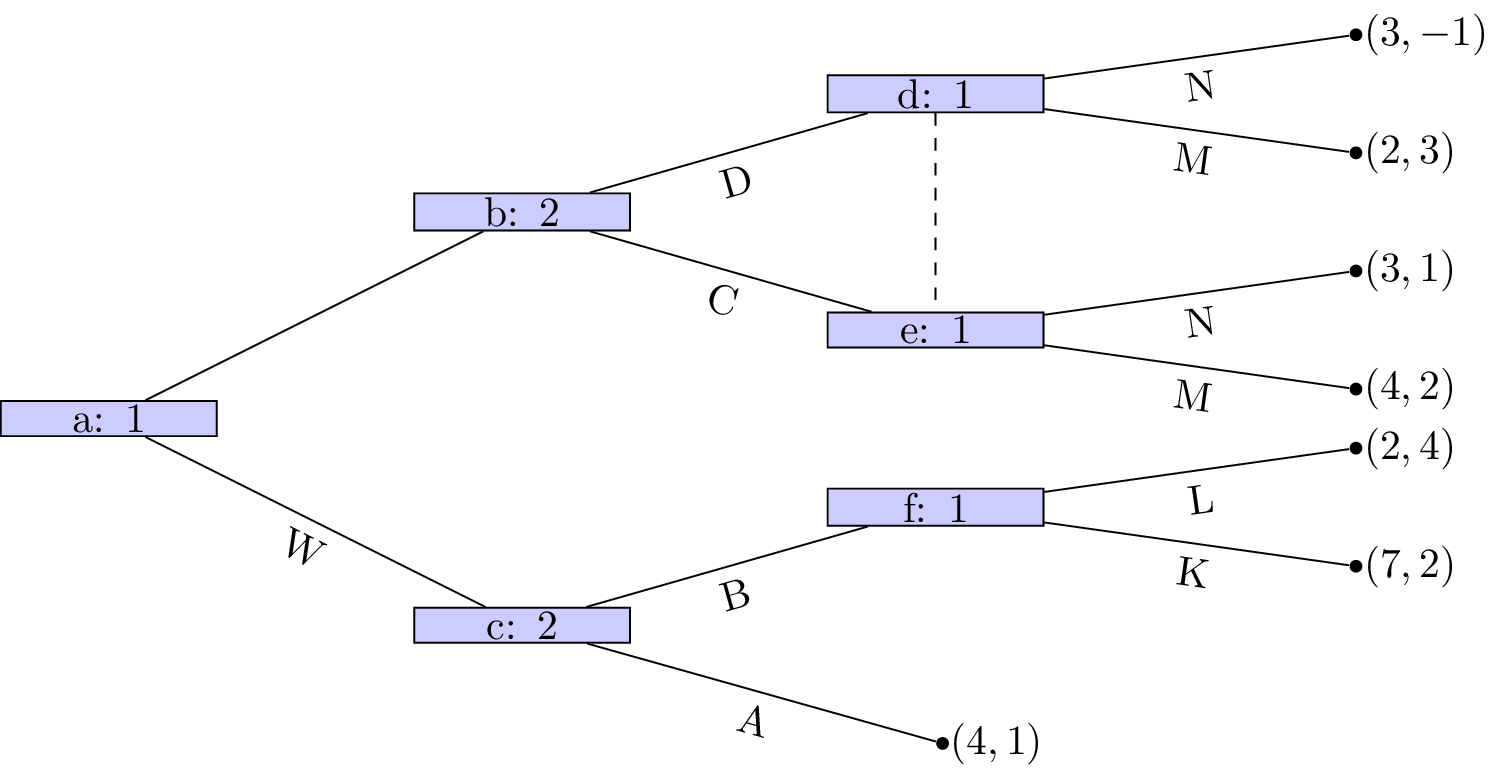
Figure 7:An extensive form game where all nodes do not initiate a subgame.
The notion of a subgame leads us to define a specific property of some Nash equilibrium.
Definition: Subgame perfect equilibrium¶
A subgame perfect Nash equilibrium is a Nash equilibrium in which the strategy profiles specify Nash equilibria for every subgame of the game.
Let us consider the example in Figure 8.
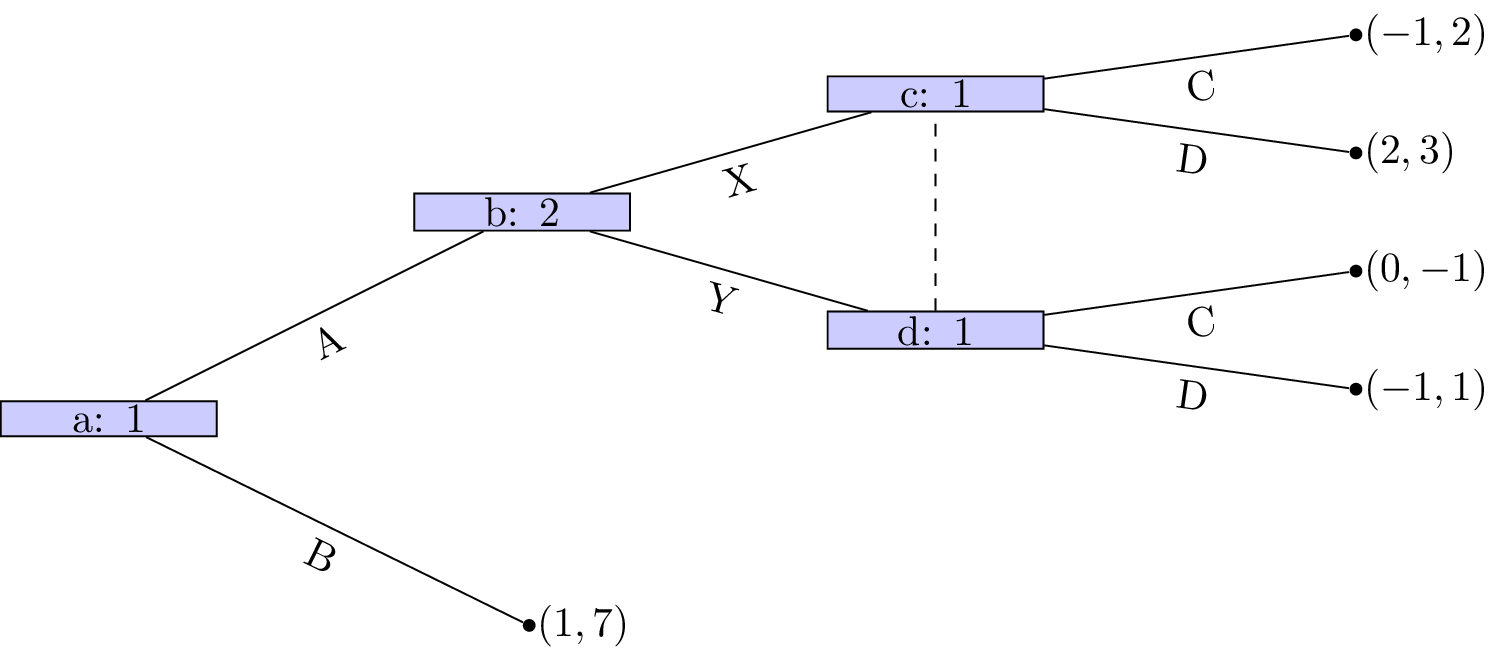
Figure 8:An game with subgame perfect equilibrium.
Let us build the corresponding normal form game:
and
using the above ordering we have:
The Nash equilibria for the above game (found by inspecting best responses in action space) are:
If we take a look at the normal form game representation of the subgame initiated at node b with action sets:
we have:
We see that the (unique) Nash equilibria for the above game is . Thus the only subgame perfect equilibria of the entire game is .
Exercises¶
Programming¶
Using Gambit to study an extensive form game¶
The pygambit library can compute equilibria of extensive form games. We define
Selten’s Chain Store Paradox as follows:
import pygambit as gbt
g = gbt.Game.new_tree(players=["Incumbent", "Entrant"],
title="1 stage Selten's Chain Store Paradox")
g.append_move(g.root, "Entrant", ["Enter", "Withdraw"])
g.append_move(g.root.children[0], "Incumbent", ["Accomodate", "Fight"])
g.set_outcome(g.root.children[1], g.add_outcome([5, 1], label="No entry"))
g.set_outcome(g.root.children[0].children[0], g.add_outcome([2, 2], label="Shared Market"))
g.set_outcome(g.root.children[0].children[1], g.add_outcome([0, 0], label="Competition"))
gThis creates the extensive form game. To convert it to a normal form:
g.to_arrays(dtype=float)[array([[2.0, 5.0],
[0.0, 5.0]], dtype=object),
array([[2.0, 1.0],
[0.0, 1.0]], dtype=object)]To compute the pure-strategy Nash equilibria:
result = gbt.nash.enumpure_solve(g)
result.equilibria[[[Rational(1, 1), Rational(0, 1)], [Rational(1, 1), Rational(0, 1)]],
[[Rational(0, 1), Rational(1, 1)], [Rational(0, 1), Rational(1, 1)]]]Notable Research¶
The concept of subgame perfection was first introduced in Selten, 1965 and later reformulated in English in Selten & Bielefeld, 1988, both by Reinhard Selten. The motivating example for this chapter—the Chain Store Paradox—appears in Selten, 1978, where Selten considers multiple sequential market entrants and examines the credibility of entry-deterrence strategies.
The framework was extended in Milgrom & Roberts, 1982, which introduced asymmetric information and reputation effects. These additions showed how players might sustain seemingly irrational threats (such as fighting entry) by considering the beliefs and inferences of future opponents.
The idea of subgame perfection was further refined in Kreps & Wilson, 1982, which introduced the concept of sequential equilibrium, and in Grossman & Perry, 1986, which developed perfect sequential equilibrium. These refinements allow for the analysis of games where off-equilibrium beliefs matter, providing stronger predictions in extensive form games with imperfect information.
Conclusion¶
Subgame perfection refines the concept of Nash equilibrium by requiring that players’ strategies form a Nash equilibrium not just in the game as a whole, but in every subgame—including those off the equilibrium path. This refinement eliminates non-credible threats and ensures sequential rationality at every decision point. Table Table 1 summaries the main concepts of this chapter.
Table 1:The main concepts for Subgame Perfectoin
| Concept | Description |
|---|---|
| Sequential rationality | Players optimise at each information set |
| Backward induction | Method to compute subgame perfect equilibria in perfect information |
| Subgame | Portion of a game starting at a decision node and fully self-contained |
| Subgame perfect equilibrium | A strategy profile that is a Nash equilibrium in every subgame |
We illustrated these ideas with Selten’s Chain Store Paradox, which highlights how subgame perfection rules out the incumbent’s non-credible threat to fight.
- Selten, R. (1978). The chain store paradox. Theory and Decision, 9(2), 127–159.
- Selten, R. (1965). Spieltheoretische behandlung eines oligopolmodells mit nachfrageträgheit: Teil i: Bestimmung des dynamischen preisgleichgewichts. Zeitschrift Für Die Gesamte Staatswissenschaft/Journal of Institutional and Theoretical Economics, H. 2, 301–324.
- Selten, R., & Bielefeld, R. S. (1988). Reexamination of the perfectness concept for equilibrium points in extensive games. Springer.
- Milgrom, P., & Roberts, J. (1982). Predation, reputation, and entry deterrence. Journal of Economic Theory, 27(2), 280–312.
- Kreps, D. M., & Wilson, R. (1982). Sequential equilibria. Econometrica: Journal of the Econometric Society, 863–894.
- Grossman, S. J., & Perry, M. (1986). Perfect sequential equilibrium. Journal of Economic Theory, 39(1), 97–119.