Motivating Example: Two Views of a Polytope¶
Consider the following set of points:
This set is a polytope, defined as the convex hull of a finite set of vertices:
A visualization is provided in Figure A1.1.
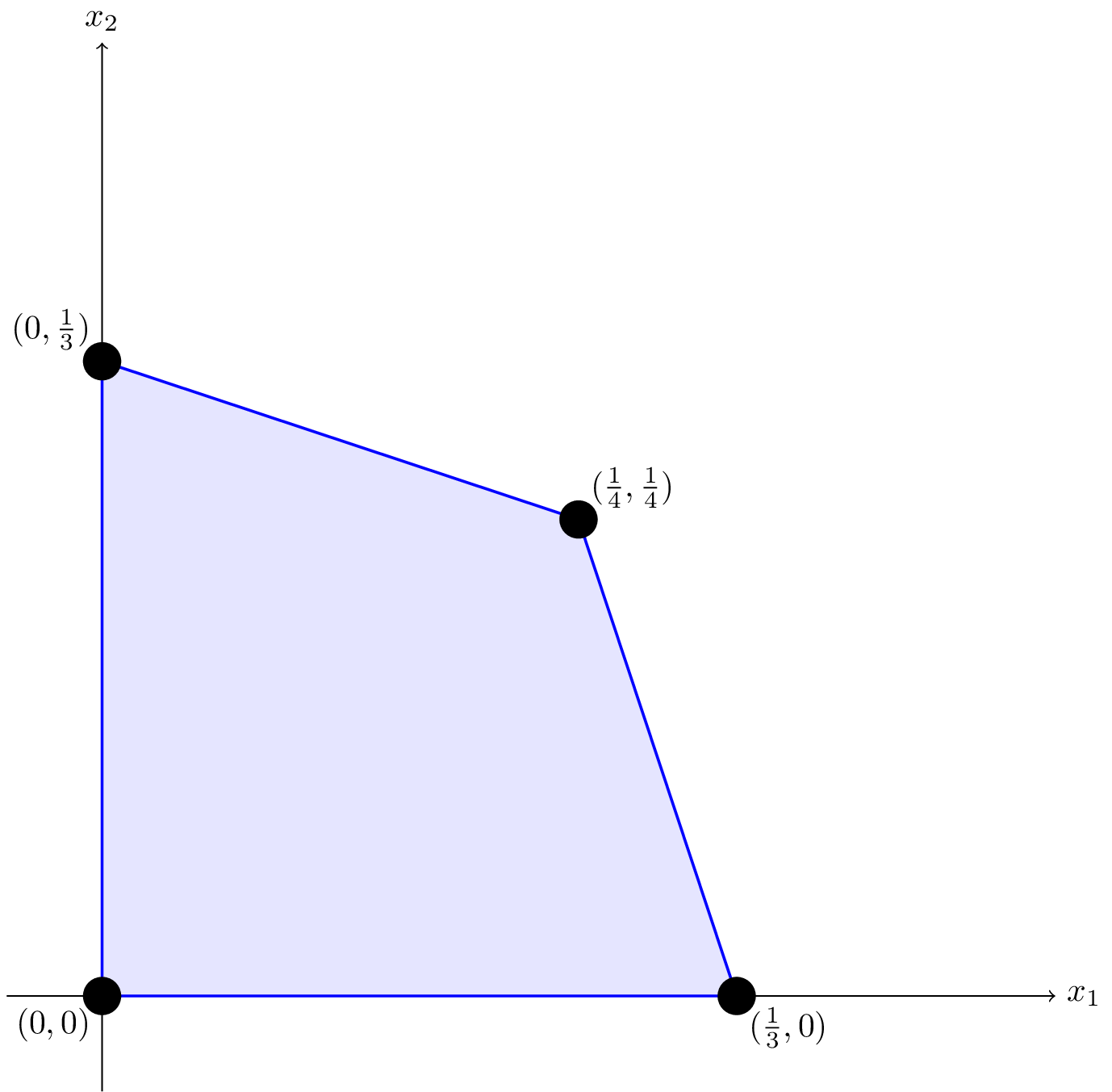
Figure A1.1:The two-dimensional polytope defined by (A1.1), shown as the convex hull of four points.
Polytopes can also be equivalently defined as the intersection of half- spaces— that is, bounded regions formed by linear inequalities. This alternate view is illustrated in Figure A1.2.
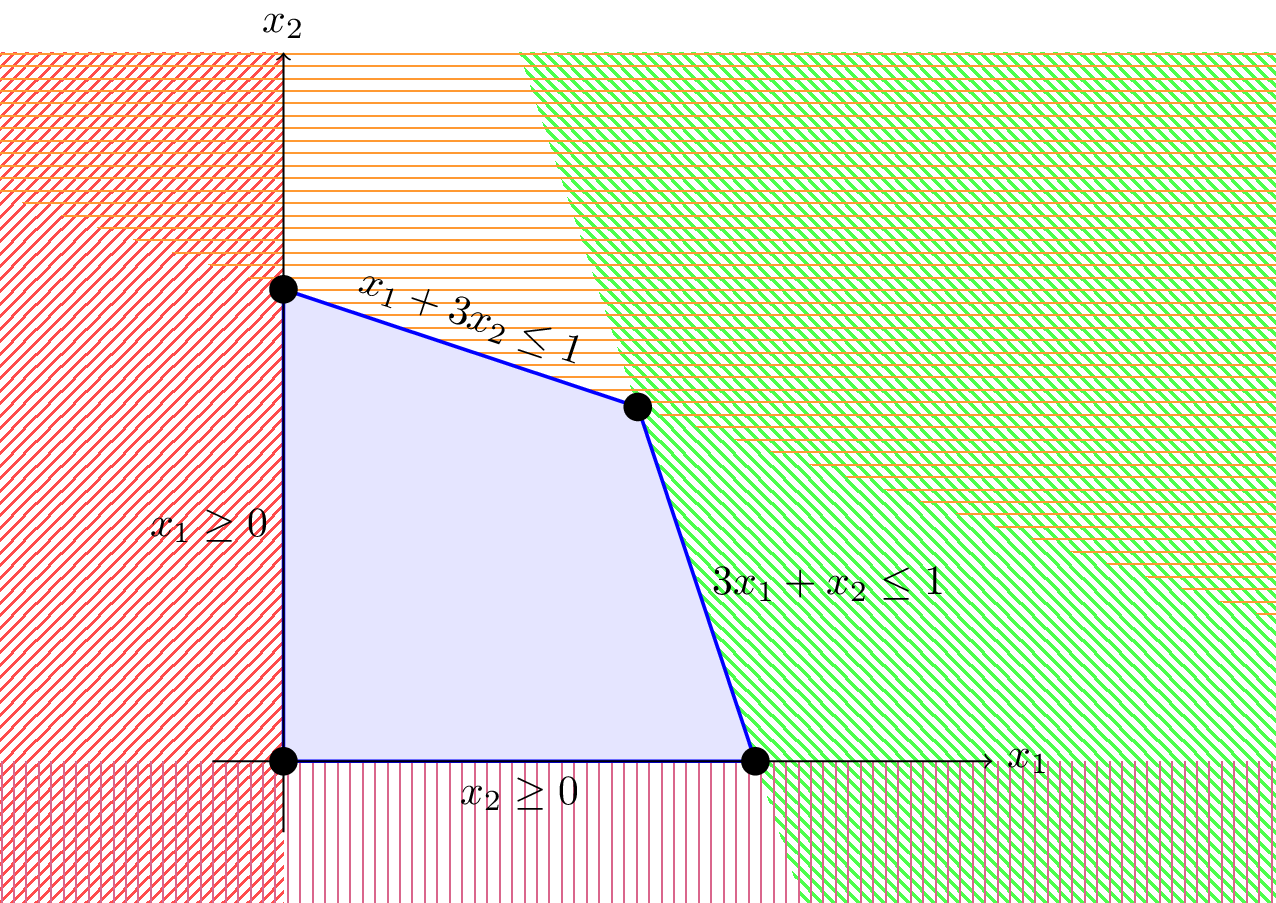
Figure A1.2:The same polytope shown in Figure A1.1, represented as the intersection of linear inequalities.
This second definition corresponds to:
The inequalities in (A1.3) define supporting half-spaces that together enclose the polytope.
Polytopes appear throughout mathematics, particularly in optimisation, where they form the feasible regions of linear programs. These connections are central to game theory, especially in the study of zero-sum games and general games.
While this example lives in , the techniques extend to higher-dimensional polytopes. The goal of this chapter is to develop tools for moving from vertex to vertex in such polytopes—an essential idea in both mathematical optimisation and algorithmic game theory.
Theory¶
Definition: Polytope as a Convex Hull¶
Let be a finite set of points. A polytope is the set of all convex combinations of points in :
Definition: Polytope as an Intersection of Half-Spaces¶
Let and . A polytope can also be defined as the set of points satisfying a system of linear inequalities:
The representation of a polytope as the intersection of half-spaces via will allow us to work efficiently with large systems.
Definition: Slack Variable¶
Given a system of linear inequalities of the form , a slack variable transforms each inequality into an equality by accounting for the difference between the left- and right-hand sides.
Formally, for each row , the inequality
can be rewritten as
where is the slack variable corresponding to the -th inequality.
Definition: Tableau Representation of Vertices¶
For and , given a system of linear inequalities:
This system of linear inequalities can be written as a system of equalities by adding slack variables to give a modified linear system of equalities:
Where and includes coefficients for the added slack variables:
Given the system a tableau is an extended matrix of the form:
This augmented matrix of the underlying linear system is used to represent points in Polytopes. Through elementary row operations which will be called pivots we can move from one vertex to another.
Example: Tableaux for the Motivating Example¶
The linear system for the Motivating Example is:
This corresponds to:
We can write a Tableau that represents the equivalent system of equations :
Tableaux are augmented matrices for linear systems, it is possible to do elementary row operations on them that do not modify the underlying system. We can also derive alternative tableaux from this example:
Multiplying 's row 1 by 3 and subtracting row 2 gives:
Multiplying 's row 2 by 8 and subtracting row 1 gives:
Multiplying 's row 1 by 9 and adding row 2 gives:
There are other tableaux that correspond to the same systems of equations but we next explore how tableaux correspond to vertices of polytopes. To do this we need a new definition:
Definition: Basic variables¶
A basic variable of a tableau corresponds a column that is linearly independent from the others.
Example: Basic variables for the different Tableaux of the Motivating Example¶
The basic variables for:
The tableau (A1.14) are the two slack variables and .
The tableau (A1.15) are and .
The tableau (A1.16) are and .
The tableau (A1.17) are and .
Thus, the non-basic variables for:
The tableau (A1.14) are and .
The tableau (A1.15) are and .
The tableau (A1.16) are and .
The tableau (A1.17) are and .
Equivalence between a tableau and a vertex¶
A tableau represents the constraints and feasible region of a polytope. A given tableau represents a vertex of the polytope.
To obtain a vertex from the tableau:
Set the non basic variables to be 0;
Solve the remaining system of equations.
Example: equivalence between tableaux and vertices¶
For (A1.14): we set the non-basic variables to 0:
The remaining linear system from the tableau is:
Note that we do not need to solve this remaining linear system as setting the non-basic variables to 0 immediately gives us the vertex: (the origin of Figure A1.1).
For (A1.15): we set the non-basic variables to 0:
The remaining linear system from the tableau is:
Solving this gives: (the bottom right vertex of Figure A1.1).
For (A1.16): we set the non-basic variables to 0:
The remaining linear system from the tableau is:
Solving this gives: (the top right vertex of Figure A1.1).
For (A1.17): we set the non-basic variables to 0:
The remaining linear system from the tableau is:
Solving this gives: (the top right vertex of Figure A1.1).
We have recovered all four vertices from the 4 tableaux of Example: Tableaux for the Motivating Example. Note that in that example through the process of applying elementary row operations to the tableaux we moved across the edges of the polytope as shown in Figure A1.3.
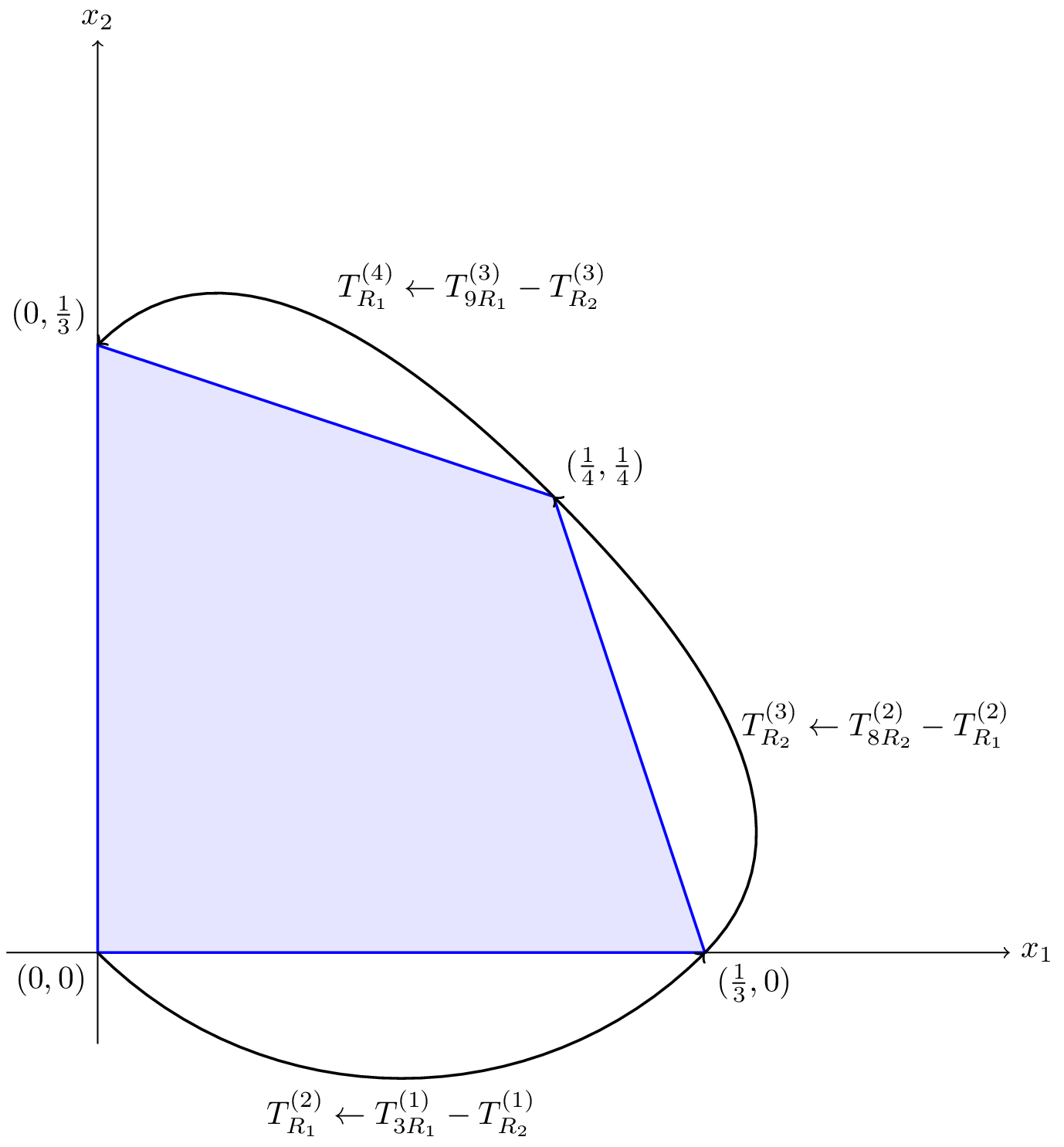
Figure A1.3:The two-dimensional polytope defined by (A1.1), with arrows showing the process of moving along the edges. The various row operations are written as short hand.
This process corresponds to making a non-basic variable basic and carefully choosing which basic variable to make non-basic.
Definition: Integer Pivoting¶
Pivoting is the process of updating a tableau by selecting one basic variable to leave the basis and one non-basic variable to enter it. This corresponds to performing row operations to rewrite the system so that the new basic variable appears with coefficient 1 in its row and 0 in all others.
In integer pivoting, we perform this process using only integer-preserving row operations, such as adding or subtracting integer multiples of rows. This is useful for maintaining exact arithmetic and geometric intuition in discrete settings.
Suppose you are given a tableau representing a system of equations and you choose a non-basic variable to enter the basis.
The goal is to perform a pivot so that becomes basic and one of the current basic variables is removed from the basis.
The pivot is carried out using the following steps:
Identify the pivot column Select the column of the tableau corresponding to .
Select the pivot row minimum ratio test For each row where the coefficient , compute the ratio:
(where corresponds to the final column of .)
Choose the row with the smallest non-negative ratio. The basic variable in this row will leave the basis.
Eliminate the pivot column in all other rows For each row , if necessary multiply it by a suitable integer multiplier and then subtract suitable integer multiples of row so that the entry in column becomes zero.
After these steps, the tableau reflects a new basic solution where is basic, and one previous basic variable has become non-basic.
Example: Moving from to ¶
Let us start at:
The non-basic variables are and . Let us choose to let become basic. This corresponds to the second column of the tableau.
Next we use the minimum ratio test:
The ratio for the first row:
The ratio for the second row:
Both of these are non-negative and the minimum value is obtained in the first row. Thus we pivot on the first row making the value in the second column and “all other rows” (in this case just the second row) 0.
Multiplying 's row 2 by 3 and subtracting row 1 gives:
Using Equivalence between a tableau and a vertex we set the basic variables to 0:
The remaining linear system from the tableau is:
Solving this gives: .
Exercises¶
Exercise: Polytope Representation¶
For each of the following sets of vertices:
Draw the corresponding polytope.
Write the polytope as the intersection of a set of halfspaces (i.e. inequalities).
Exercise: Basic and Non-Basic Variables¶
For each of the following tableaux, identify the basic and non-basic variables:
Exercise: Integer Pivoting¶
For the tableaux in Exercise: Basic and Non-Basic Variables (insert reference):
For each non-basic variable, perform one step of integer pivoting:
Identify the pivot column;
Perform the minimum ratio test to determine the pivot row;
Execute the required row operations to complete the pivot.
Programming¶
Using SciPy to obtain the convex hull¶
The SciPy library has functionality to obtain the convex hull of a set of vertices.
import scipy.spatial
import numpy as np
V = [np.array([0, 0]), np.array([1 / 3, 0]), np.array([1 / 4, 1 / 4]),
np.array([0, 1 / 3])]
P = scipy.spatial.ConvexHull(V)
scipy.spatial.convex_hull_plot_2d(P);
The obtained convex hull can be used to get the system of linear inequalities:
P.equationsarray([[-0. , -1. , 0. ],
[-1. , 0. , -0. ],
[ 0.9486833 , 0.31622777, -0.31622777],
[ 0.31622777, 0.9486833 , -0.31622777]])Using SciPy to obtain the half space¶
The Scipy library has functionality to obtain the vertices from a given intersection of half spaces.
First we create the system of linear inequalities , this is done passing: as single matrix
halfspace = np.array(
(
(-1, 0, 0),
(0, -1, 0),
(3, 1, -1),
(1, 3, -1),
)
)We need to pass a point known to be in the interior of the Polytope. Now we can obtain the vertices the original vertices from (A1.1).
P = scipy.spatial.HalfspaceIntersection(halfspace, interior_point=np.array((1/5,
1/5)))
P.intersectionsarray([[2.77555756e-17, 3.33333333e-01],
[2.50000000e-01, 2.50000000e-01],
[0.00000000e+00, 0.00000000e+00],
[3.33333333e-01, 2.77555756e-17]])Carrying out row operations using NumPy¶
NumPy’s linear array gives allows for straightforward row operations.
T_1 = np.array(
(
(1, 3, 1, 0, 1),
(3, 1, 0, 1, 1),
)
)
T_2 = T_1
T_2[0] = 3 * T_2[0] - T_2[1]
T_2array([[ 0, 8, 3, -1, 2],
[ 3, 1, 0, 1, 1]])Pivoting tableaux with Nashpy¶
NashPy has some internal functionality for integer pivoting, which at present is not designed to be user facing but is nonetheless useable:
import nashpy as nash
T = nash.linalg.Tableau(T_2)Having created this tableau we can get the indices of the basic and non-basic variables:
T.basic_variables{0, 2}T.non_basic_variables{np.int64(1), np.int64(3)}We can pivot the tableau on a given column and given row:
T._pivot(column_index=1, pivot_row_index=1)This pivoted on the first column returning which non-variable becomes basic as a result.
We can look at the tableau:
T._tableauarray([[-24, 0, 3, -9, -6],
[ 3, 1, 0, 1, 1]])Notable Research¶
The concept of pivoting and tableaux was first introduced by the mathematician George Dantzig in a 1947 report during his tenure at the Pentagon Dantzig, 1947.
The initial publication of this idea is found in Dantzig, 1951. Although Dantzig did not explicitly mention tableaux, they naturally emerged as an efficient method for traversing the edges of a polytope.
In Dantzig, 2020 (originally published in 1990), Dantzig shares the following anecdote:
"The first idea that would occur to anyone as a technique for solving a linear program, aside from the obvious one of moving through the interior of the convex set, is that of moving from one vertex to the next along the edges of the polyhedral set. I discarded this idea immediately as impractical in higher dimensional spaces. It seemed intuitively obvious that there would be far too many vertices and edges to wander over in the general case for such a method to be efficient.
When Hurwicz came to visit me at the Pentagon in the summer of 1947, I told him how I had discarded this vertex-edge approach as intuitively inefficient for solving LP. I suggested instead that we study the problem in the geometry of columns rather than the usual one of the rows -- column geometry incidentally was the one I had used in my Ph.D. thesis on the Neyman-Pearson Lemma. We dubbed the new method ‘climbing the bean pole.’"
A comprehensive historical overview is provided in Todd, 2002, which includes several other notable publications.
Two significant works connect integer pivoting to game theory:
In a 1951 book chapter, Dantzig established a connection for zero-sum games, as described in Adler, 2013.
Lemke & Howson, 1964 introduces the Lemke-Howson algorithm, which employs integer pivoting to find Nash equilibria in general games.
Conclusion¶
Integer pivoting offers a powerful lens through which to understand movement across the vertices of polytopes, providing a concrete foundation for key algorithms in linear programming and game theory. Through the tableau representation, we are able to:
Translate systems of inequalities into algebraic form;
Perform exact row operations that correspond to movement along polytope edges;
Interpret basic and non-basic variables as defining vertices and directions of movement.
This chapter has introduced the core tools required to navigate these geometric structures, setting the stage for applications in zero-sum games and Nash equilibrium computation.
Table A1.1 summarises the key concepts introduced in this appendix.
Table A1.1:Summary of integer pivoting
| Concept | Description |
|---|---|
| Polytope (convex hull) | Set of convex combinations of finite points |
| Polytope (half-spaces) | Set of solutions to a system of linear inequalities |
| Slack variable | Converts an inequality into an equality with a non-negative remainder |
| Tableau | Augmented matrix form of a linear system with slack variables |
| Basic variable | Variable corresponding to a pivot column; used to determine a vertex |
| Non-basic variable | Set to 0 when solving for vertex from tableau |
| Pivoting | Row operations used to exchange basic and non-basic variables |
| Minimum ratio test | Selects the pivot row to preserve feasibility during a pivot |
| Integer pivoting | Pivoting using only integer row operations to maintain exact structure |
- Dantzig, G. B. (1947). Maximization of a Linear Function of Variables Subject to Linear Inequalities (Techreport P-38). Rand Corporation.
- Dantzig, G. B. (1951). Maximization of a linear function of variables subject to linear inequalities. Activity Analysis of Production and Allocation, 13, 339–347.
- Dantzig, G. B. (2020). Impact of linear programming on computer development. In Computers in Mathematics (pp. 233–240). CRC Press.
- Todd, M. J. (2002). The many facets of linear programming. Mathematical Programming, 91(3), 417–436.
- Adler, I. (2013). The equivalence of linear programs and zero-sum games. International Journal of Game Theory, 42, 165–177.
- Lemke, C. E., & Howson, J. T., Jr. (1964). Equilibrium points of bimatrix games. Journal of the Society for Industrial and Applied Mathematics, 12(2), 413–423.