Motivating Example: Competing delivery companies¶
In a busy city, two rival delivery companies — QuickShip and TurboExpress — operate daily distribution routes to deliver packages to the central business district.
Each company starts from its own warehouse, located in different suburbs on opposite sides of the city. Every morning, the companies dispatch their fleets toward the central depot, but must decide how to route their vans:
Each company can take its own dedicated service road to the depot.
Alternatively, both companies can use a shared ring road that offers a faster connection, but becomes congested as total traffic increases.
The travel costs for each route depend on the level of congestion:
For QuickShip (source ):
Dedicated service road cost: , where is the number of QuickShip vans using this road.
For TurboExpress (source ):
Dedicated service road cost: .
For the shared ring road (available to both companies):
Shared road cost: , where is the total number of vans from both companies using this route.
Each source has a total demand of units of traffic to send to the sink.
This is shown diagrammatically in Figure 1.
Each company decides independently how to distribute its fleet across the available routes, aiming to minimise its own delivery costs. However, since the shared road’s cost depends on total usage, each company’s decision affects the other’s outcome.
This setting creates a routing game, where decentralised decisions lead to interdependent costs. We will analyse this scenario to explore the concept of Nash equilibrium in network routing, and investigate how self-interested routing can result in stable, but potentially inefficient, traffic patterns.
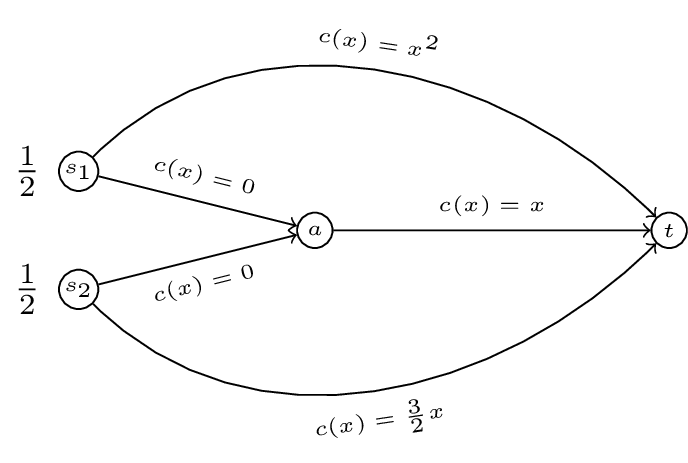
Figure 1:The routes available to QuickShip and TurboExpress.
Theory¶
Definition: Routing Game¶
A routing game is defined on a graph with a defined set of sources and sinks . Each source-sink pair corresponds to a set of traffic (also called a commodity) that must travel along the edges of from to . Every edge of has associated to it a nonnegative, continuous and nondecreasing cost function (also called latency function) .
Example: The Routing Game Representation of the Delivery Companies Game¶
For the routing game in Figure 1:
with and
Definition: Set of Paths¶
For any given we denote by the set of paths available to commodity .
Definition: Feasible Flow¶
On a routing game we define a flow as a vector representing the quantity of traffic along the various paths, is a vector index by . Furthermore we call feasible if:
Example: Feasible Flows for the Delivery Companies Game¶
For the routing game in Figure 1:
and
The set of all possible paths is denoted by .
Definition: Cost function¶
For any routing game we define a cost function :
Where denotes the cost function of a particular path : . Note that any flow induces a flow on edges:
So we can re-write the cost function as:
Example: Cost function for the Delivery Companies Game¶
For the routing game in Figure 1:
Let as shown in Figure 2.
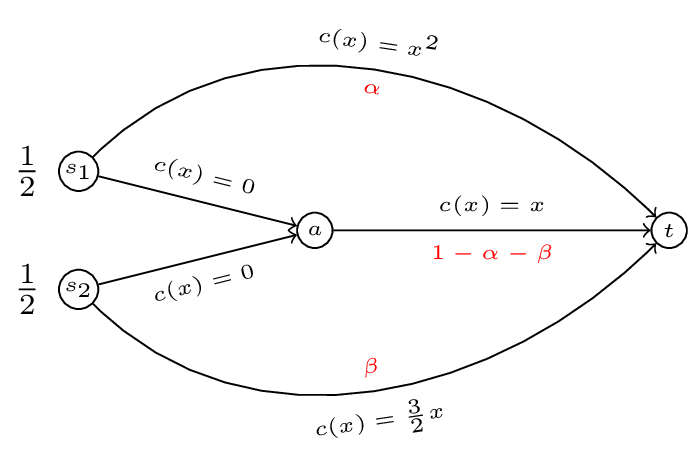
Figure 2:The vector showing the flow on the game
The cost of is given by:
Definition: Optimal Flow¶
For a routing game we define the optimal flow as the solution to the following optimisation problem:
Minimise :
Subject to:
Example: Optimal Flow for the Delivery Companies Games¶
In Figure 2 this corresponds to:
Minimise :
Subject to:
A plot of is shown in Figure 3.
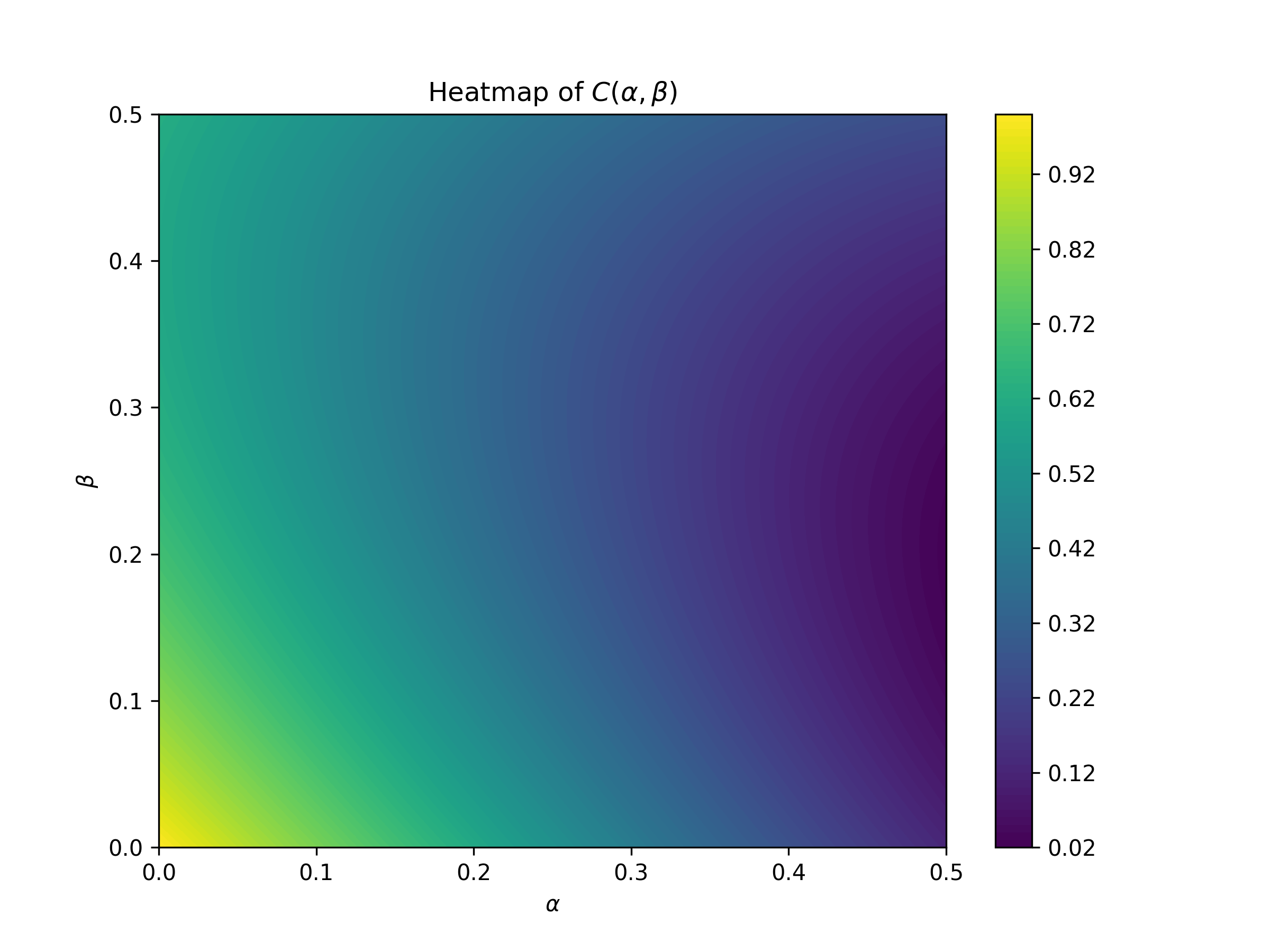
Figure 3:The plot of .
The minimal point looks to be near the right boundary of the square, although it is unclear if it is on the boundary or not. It is in fact not on the boundary taking this fact as an assumption, identity the optimal flow using the Karush-Kuhn-Tucker conditions.
Let us first define the Lagrangian:
If is the minimal point then the complementary slackness implies that for all , since this point does not sit on any boundary which would make the corresponding constraint function .
Thus:
We note that the feasiblity constraints all hold for so we are left to check stationarity:
and
which gives:
Substituting this in to the first equation gives:
which has solutions:
Only one of those is positive satisfying the constraints, substituting it in to (14) gives:
thus the optimal flow is:
If we take a closer look at in our example, we see that traffic from the first commodity travels across two paths: and . The cost along the first path is given by:
The cost along the second path is given by:
Thus traffic going along the second path is experiencing a higher cost. In practice, they would deviate some of their traffic from the second path to the first.
This leads to the definition of a Nash flow.
Definition: Nash Flow¶
For a routing game a flow is called a Nash flow if and only if for every commodity and any two paths such that then:
A Nash flow ensures that all used paths have minimal costs.
Example: Nash Flow for Delivery companies game¶
For Figure 2 if we assume that both commodities use all paths available to them:
Solving this gives: this gives
Neither of these two values are within our region thus there is no Nash flow where all paths are used.
Let us assume that (i.e. commodity 1 does not use ). Assuming that the second commodity uses both available paths we have:
Thus we have which gives a cost of which is higher than the optimal cost!
What if we had assumed that ?
This would have given which has solutions:
Taking the second value for which does lie in the feasible region. The cost of the path is then approximately .134 however the cost of the path is approximately .75 thus the second commodity should deviate. We can carry out these same checks with all other possibilities to verify that is a Nash flow.
Definition: Potential Function¶
Given a routing game we define the potential function of a flow as:
Example: Potential Function for the delivery company game¶
The potential function for Figure 2 is given by:
Theorem: Nash Flow minimises the potential function¶
A feasible flow is a Nash flow for the routing game if and only if it is a minima for .
Definition: Marginal Cost¶
If is a differentiable cost function then we define the marginal cost function as:
Example: The marginal costs for the delivery company game¶
The marginal costs for Figure 2 are given by:
The corresponding routing game is shown in Figure 4.
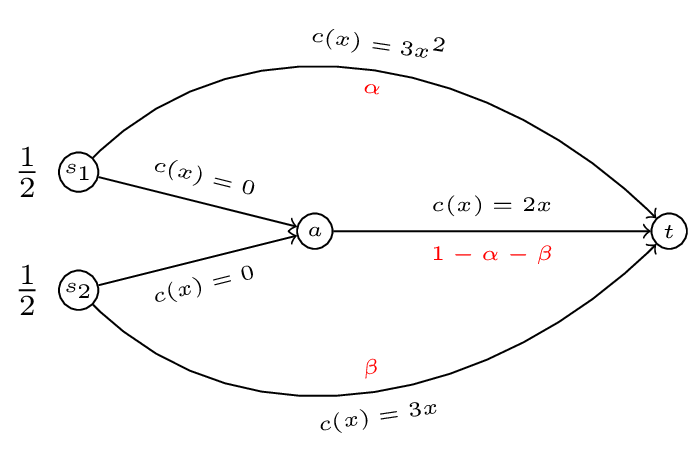
Figure 4:The routes available to QuickShip and TurboExpress with marginal costs instead of costs.
Theorem: Optimal Flow is a Nash Flow for Marginal Costs¶
A feasible flow is an optimal flow for if and only if is a Nash flow for .
Exercises¶
Programming¶
Scipy has functionality for optimising function within certain boundaries, thanks to Theorem: Nash Flow minimises the potential function this can be used to find not only optimal flows but also Nash flows.
In Appendix: Karush-Kuhn-Tucker Conditions is an example showing how to use Scipy to optimise a function. Here is another one:
import numpy as np
import scipy.optimize
def objective(f):
alpha, beta = f
return alpha ** 3 / 3 + 3 * beta ** 2 / 4 + (1 - alpha - beta) ** 2 / 2
def g_1(f):
return f[0]
def g_2(f):
return f[1]
def g_3(f):
return 1 / 2 - f[0]
def g_4(f):
return 1 / 2 - f[1]
constraints = [
{'type': 'ineq', 'fun': g_1},
{'type': 'ineq', 'fun': g_2},
{'type': 'ineq', 'fun': g_3},
{'type': 'ineq', 'fun': g_4},
]
res = scipy.optimize.minimize(objective, [0, 0], constraints=constraints)
res message: Optimization terminated successfully
success: True
status: 0
fun: 0.11666666666666675
x: [ 5.000e-01 2.000e-01]
nit: 4
jac: [-5.000e-02 -9.313e-10]
nfev: 12
njev: 4
multipliers: [ 0.000e+00 0.000e+00 5.000e-02 0.000e+00]Notable Research¶
The original paper introducing the notion of Nash flows is Wardrop, 1952. An important phenomenon in this field is Braess’s Paradox, first described in Braess, 1968, which shows that adding capacity to a network can paradoxically increase overall congestion. This effect is not purely theoretical and has been observed in real-world settings Steinberg & Zangwill, 1983Youn et al., 2008.
The inefficiencies that arise in congestion networks due to self-interested behaviour have led to the concept of the Price of Anarchy, defined as . This concept was introduced in Roughgarden & Tardos, 2002. Various applications have been explored, including Knight & Harper, 2013, which studied the inefficiencies caused by patients selecting hospitals based on individual preferences.
Conclusion¶
In this chapter, we introduced routing games, where self-interested agents choose paths through a network to minimize their own travel costs. These individual decisions create congestion effects, making costs interdependent and leading to potentially inefficient outcomes.
We developed a formal framework for routing games, introduced the key concepts of feasible flow, optimal flow, and Nash flow, and explored how potential functions allow us to compute Nash flows via standard optimisation techniques. We also introduced the concept of marginal costs, leading to the result that optimal flows correspond to Nash flows in a modified game with marginal cost functions.
Table 1 summarises the key concepts introduced in this chapter.
Table 1:Summary of routing games
| Concept | Definition |
|---|---|
| Feasible Flow | Any flow satisfying demand and non-negativity constraints |
| Optimal Flow () | Flow minimizing the total system cost $C(f)$ |
| Nash Flow () | Flow where no player can reduce their cost by unilaterally switching routes |
| Potential Function | |
| Marginal Cost |
- Wardrop, J. G. (1952). Some theoretical aspects of road traffic research. Proceedings of the Institution of Civil Engineers, 1(5), 767–768.
- Braess, D. (1968). Über ein Paradoxon aus der Verkehrsplanung. Unternehmensforschung, 12, 258–268.
- Steinberg, R., & Zangwill, W. I. (1983). The prevalence of Braess’ paradox. Transportation Science, 17(3), 301–318.
- Youn, H., Gastner, M. T., & Jeong, H. (2008). Price of anarchy in transportation networks: efficiency and optimality control. Physical Review Letters, 101(12), 128701.
- Roughgarden, T., & Tardos, É. (2002). How bad is selfish routing? Journal of the ACM (JACM), 49(2), 236–259.
- Knight, V. A., & Harper, P. R. (2013). Selfish routing in public services. European Journal of Operational Research, 230(1), 122–132.