What is Game Theory?¶
A common definition of the subject is:
“Game theory is the study of interactive decision-making where the outcomes of one decision maker’s choices depend on the decisions made by others.”
While this definition captures the essence of strategic interaction, game theory is much more than that. It is a beautiful mathematical discipline with deep theoretical avenues for exploration. It plays a crucial role in the global economy, with multiple Nobel Prizes awarded for contributions to our understanding of markets. It provides models that explain how biological structures, from cells to ecosystems, evolve over time. It offers insights into cooperation, competition, and the formation of social norms.
Because game theory spans multiple disciplines, no single definition fully captures its scope. This book aims to provide a solid understanding of game theory: what it can do and how to apply it.
Who is this book for?¶
This book is written primarily for advanced undergraduate mathematicians and computer scientists. It may also serve as a starting point for early-career researchers seeking a practical understanding of game theory.
However, the book aims to be accessible to aspiring game theorists from any discipline. A psychologist modeling a specific behavior? A conservationist analyzing the conditions under which a policy is likely to succeed? An economist studying strategic interactions in competitive markets? A computer programmer implementing a game-theoretic algorithm? Whatever your background, this book provides the necessary tools to engage with game theory in a meaningful way.
The book includes four appendices that introduce mathematical theory independently of game theory. For some readers, these may serve as a review of familiar topics, while for others, they offer a first introduction to key techniques needed to apply game-theoretic ideas effectively.
Each chapter includes a section demonstrating how software can be used to apply the ideas at scale. These sections assume some familiarity with Python and the ability to install external libraries. For an introduction to these topics, see the chapters on Using Notebooks and Installing Libraries in the Python for Mathematics text.
Game theory is a field that thrives on cross-disciplinary insights, and this book is designed to help readers from different backgrounds develop a shared mathematical foundation. Whether your interest is theoretical or applied, the goal is to equip you with the tools to explore game theory with confidence.
How is this book different from similar books?¶
There are a number of excellent books on game theory that are highly recommended. For a fantastic introduction to the topic aimed at a mathematical audience, see Webb, 2007. The exhaustive work Maschler et al., 2020 offers a vast amount of breadth and depth on the subject, while Roughgarden, 2010 delves into modern algorithmic approaches to modeling complex systems at an advanced level.
Some excellent texts focus on specific subtopics within the domain. For example, Gusfield & Irving, 1989 explores matching games, and Roughgarden, 2002 addresses routing games. Other great general introductions include Osborne & others, 2004, Watson, 2002, and Gusfield & Irving, 1989, to name just a few.
This book, however, offers something that these fantastic works do not: detailed implementation instructions, including multiple examples and exercises that show how to solve specific problems, even when they are large and complex. Additionally, it provides an overview of open-source software tools that are readily available to solve real-world problems. The book also includes discussion of relevant contemporary research aiming to demonstrate not only how the topic is applied in practice but also its relevance. Finally, it offers a rigorous theoretical foundation, serving as a springboard for deeper theoretical analysis.
How is this book organised?¶
Each chapter in this book follows a structured format:
A motivating case study: a running example throughout the chapter to illustrate and contextualize the theory, often drawing from real-world scenarios.
Relevant definitions and theory: providing a rigorous mathematical foundation for the chapter’s topic.
Exercises: a range of problems inviting the reader to apply the definitions and theory to deepen understanding.
Practical implementations: including Python code, and an overview of relevant open-source tools to guide implementation.
Contemporary research: a hand-picked, non-exhaustive overview of relevant research related to the chapter.
Some readers may prefer to focus on the theoretical foundations, while others might engage primarily with the examples and practical implementations. This book is designed to be flexible, allowing readers to approach the material in a way that best suits their background and interests.
Figure 1 shows the general structure of the book and how the various chapters link together.
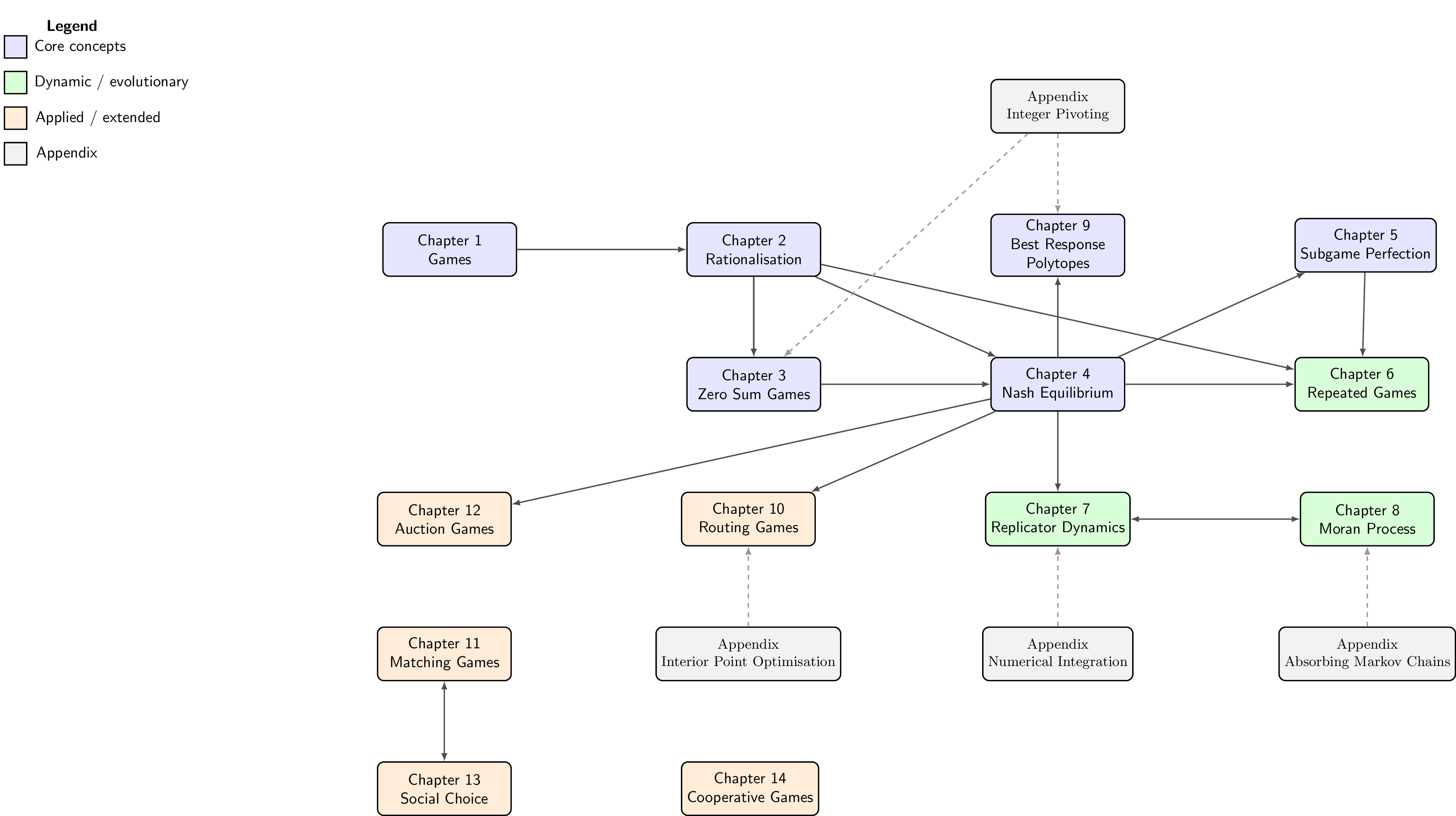
Figure 1:Visual representation of the relationships and flow between chapters.
- Webb, J. N. (2007). Game theory: decisions, interaction and Evolution. Springer Science & Business Media.
- Maschler, M., Zamir, S., & Solan, E. (2020). Game theory. Cambridge University Press.
- Roughgarden, T. (2010). Algorithmic game theory. Communications of the ACM, 53(7), 78–86.
- Gusfield, D., & Irving, R. W. (1989). The stable marriage problem: structure and algorithms. MIT press.
- Roughgarden, T. A. (2002). Selfish routing. Cornell University.
- Osborne, M. J., & others. (2004). An introduction to game theory (Vol. 3). Springer.
- Watson, J. (2002). Strategy: an introduction to game theory. (No Title).