Using the two thirds of the average game in class
This past week I have been delighted to have a short pedagogic paper accepted for publication in MSOR Connections. The paper is entitled: “Playing Games: A Case Study in Active Learning Applied to Game Theory”. The journal is open access and you can see a pre print here. As well as describing some literature on active learning I also present some data I’ve been collecting (with the help of others) as to how people play two subsequent plays of the two thirds of the average game (and talk about another game also).
In this post I’ll briefly put up the results here as well as mention a Python library I’m working on.
If you’re not familiar with it, the two thirds of the average game asks players to guess a number between 0 and 100. The closest number to 2/3rds of the average number guessed is declared the winner.
I use this all the time in class and during outreach events. I start by asking participants to play without more explanation than the basic rules of the game. Following this, as a group we go over some simple best response dynamics that indicate that the equilibrium play for the game is for everyone to guess 0. After this explanation, everyone plays again.
Below you can see how this game has gone as a collection of all the data I’ve put together:
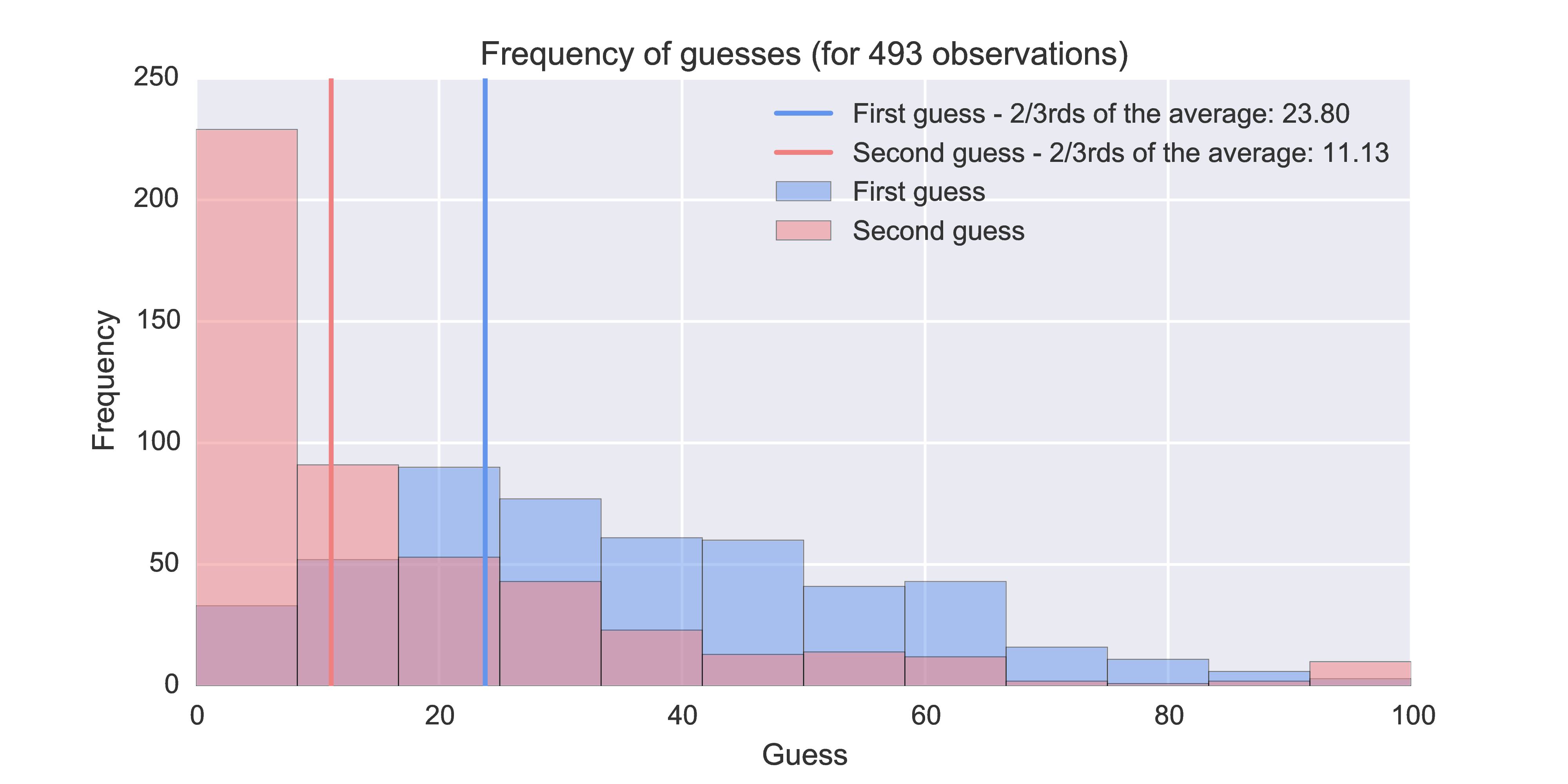
You will note that some participants actually increase their second guess but in general we see a possible indication (based on two data points, so obviously this is not meant to be a conclusive statement) of convergence towards the theoretic equilibria.
Here is a plot showing the relationship between the first and second guess (when removing the guesses that increase, although as you can see in the paper this does not make much difference):
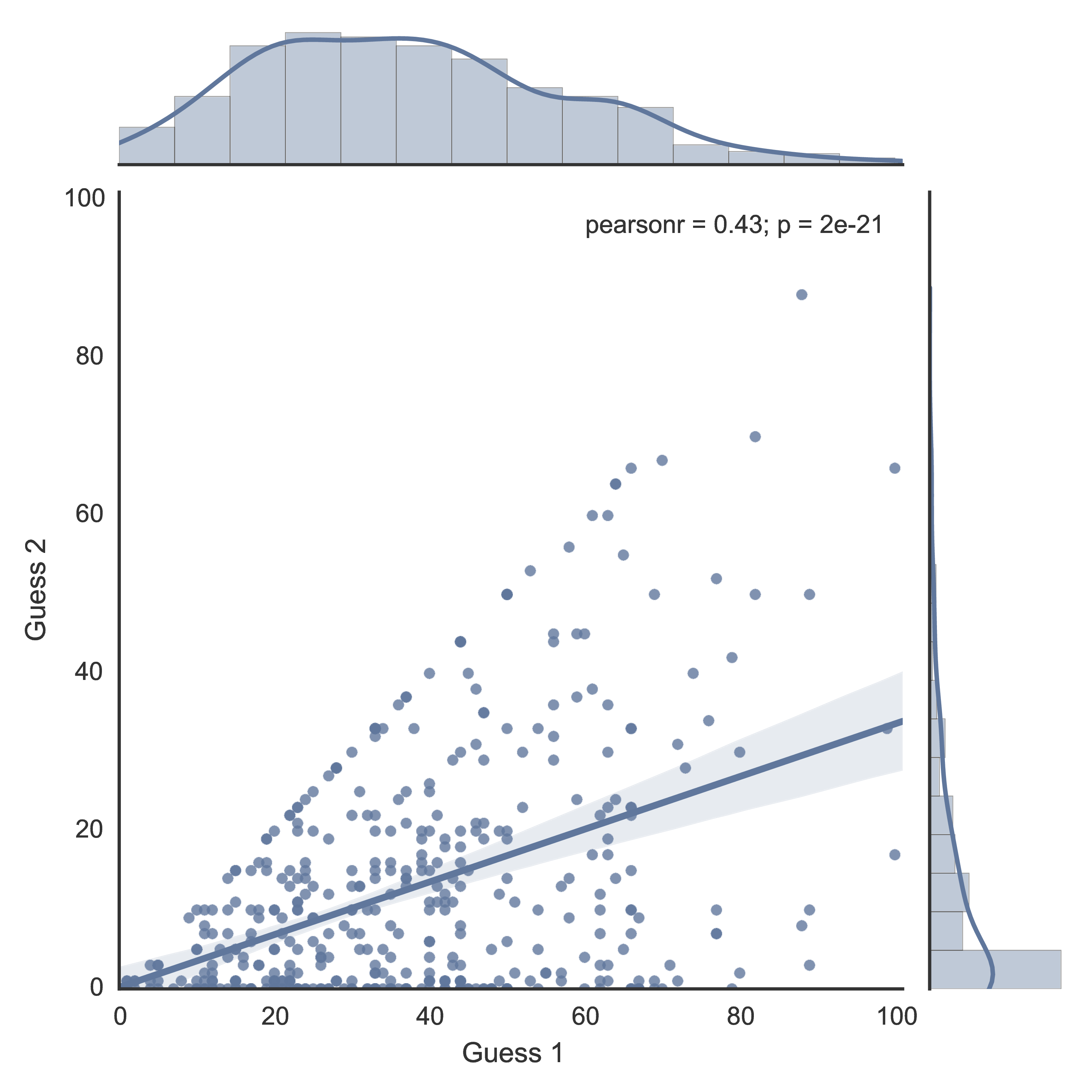
The significant linear relationship between the guesses is given by:
So a good indication of what someone will guess in the second round is that it would be a third of their first round guess.
Here is some Sage code that produces the cobweb diagram assuming the following sequence represents each guess (using code by Marshall Hampton):
that plot shows the iterations of the hypothetical guesses if we were to play more rounds :)
The other thing I wanted to point at in this blog post is this twothirds library which will potentially allow anyone to analyse these games quickly. I’m still working on it but if it’s of interest please do jump in :) I have put up a Jupyter notebook demoing what it can do so far (which is almost everything but with some rough edges). If you want to try it out, download that notebook and run:
$ pip install twothirdsI hope that once the library is set up anyone who uses it could simply send over data of game plays via PR which would help update the above plots and conclusions :)