Playing stochastic games in class
The final blog post I am late in writing is about the Stochastic game we played in class last week. The particular type of game I am referring to is also called a Markov game where players play a series of Normal Form games, with the next game being picked from a random distribution the nature of which depends on the strategy profiles. In other words the choice of the players does not only impact on the utility gained by the players but also on the probability of what the net game will be… I blogged about this last year so feel free to read about some of the details there.
The main idea is that one stage game corresponds to this normal form game (a prisoner’s dilemma):
at the other we play:
The probability distributions, of the form \((x,1-x)\) where \(x\) is the probability with which we play the first game again are given by:
and the probability distribution for the second game was \((0,1)\). In essence the second game was an absorption game and so players would try and avoid it.
To deal with the potential for the game to last for ever we played this with a discounting factor \(\delta=1/2\). Whilst that discounting factor will be interpreted as such in theory, for the purposes of playing the game in class we used that as a probability at which the game continues.
You can see a photo of this all represented on the board:

We played this as a team game and you can see the results here:
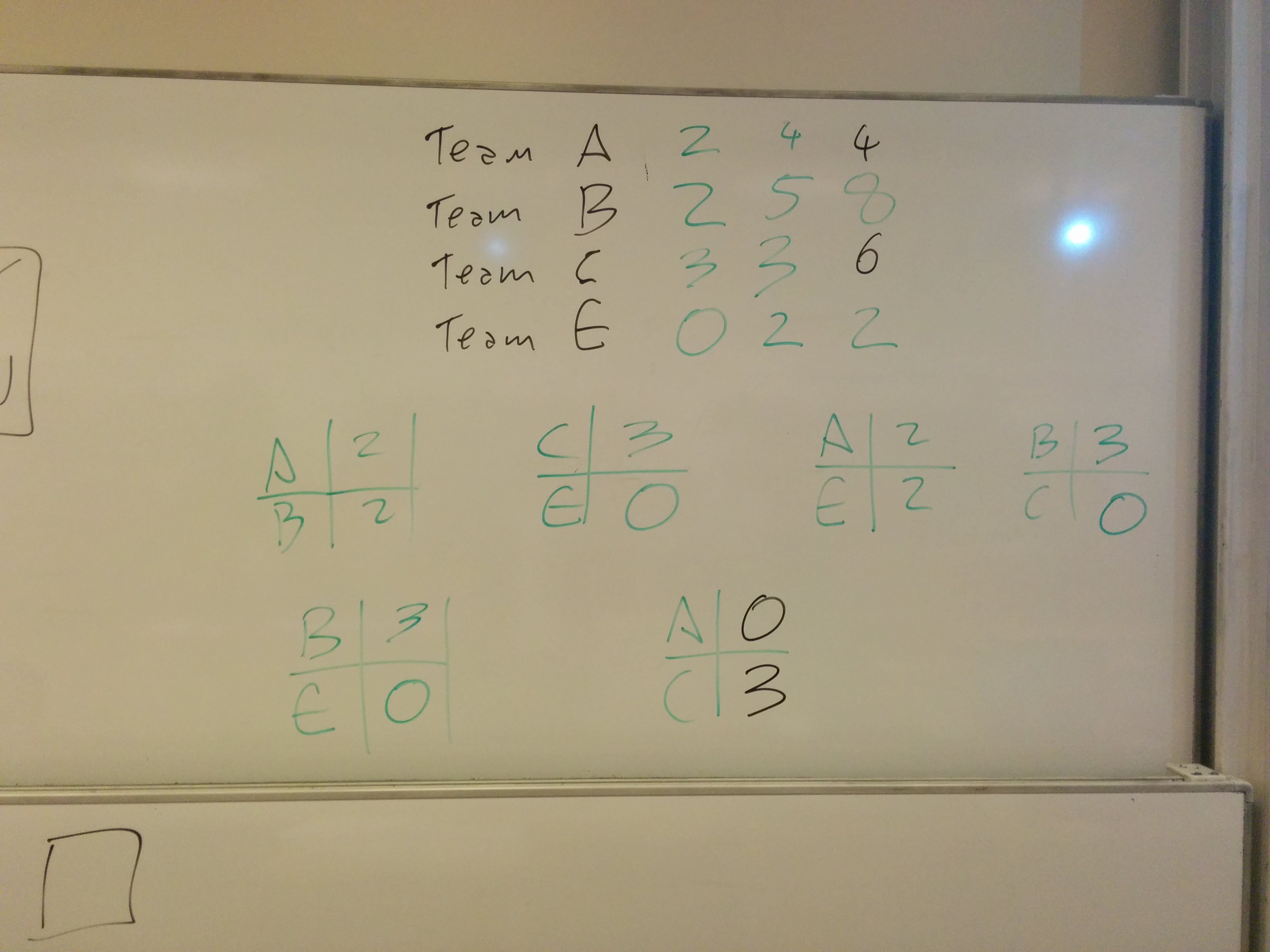
As opposed to last year no actual duel lasted more than one round: I had a coded dice to sample at each step. The first random roll of the dice was to see if the game continued based on the \(\delta\) property (this in effect ‘deals with infinity’). The second random sample was to find out which game we payed next and if we ever went to the absorption games things finished there.
The winner was team B who in fact defected after the initial cooperation in the first game (perhaps that was enough to convince other teams they would be cooperative).
After playing this, we calculated (using some basic algebra examining each potential pure equilibria) the Nash equilibria for this game and found that there were two pure equilibria: both players Cooperating and both players defecting.