Playing an infinitely repeated game in class
Following the iterated Prisoner’s dilemma tournament my class I and I played last week we went on to play a version of the game where we repeated things infinitely many times. This post will briefly describe what we got up to.
As you can read in the post about this activity from last year, the way we play for an infinite amount of time (that would take a while) is to apply a discounting factor \(\delta\) to the payoffs and to interpret this factor as the probability with which the game continues.
Before I go any further (and put up pictures with the team names) I need to explain something (for the readers who are not my students).
For every class I teach I insist in spending a fair while going over a mid module feedback form that is used at Cardiff University (asking students to detail 3 things they like and don’t like about the class). One student wrote (what is probably my favourite piece of feedback ever):
“Vince is a dick… but in a good way.”
Anyway, I mentioned that to the class during my feedback-feedback session and that explains one of the team names (which I found pretty amusing):
- Orange
- Where’s the gun
- We don’t know
- Vince is a good dick
Once we had the team names set up (and I stopped trying to stop laughing) I wrote some quick Python code that we could run after each iteration:
import random
continue_prob = .5
if random.random() < continue_prob:
print 'Game continues'
else:
print 'Game Over'We started off by playing with (\delta=.5) and here are the results:
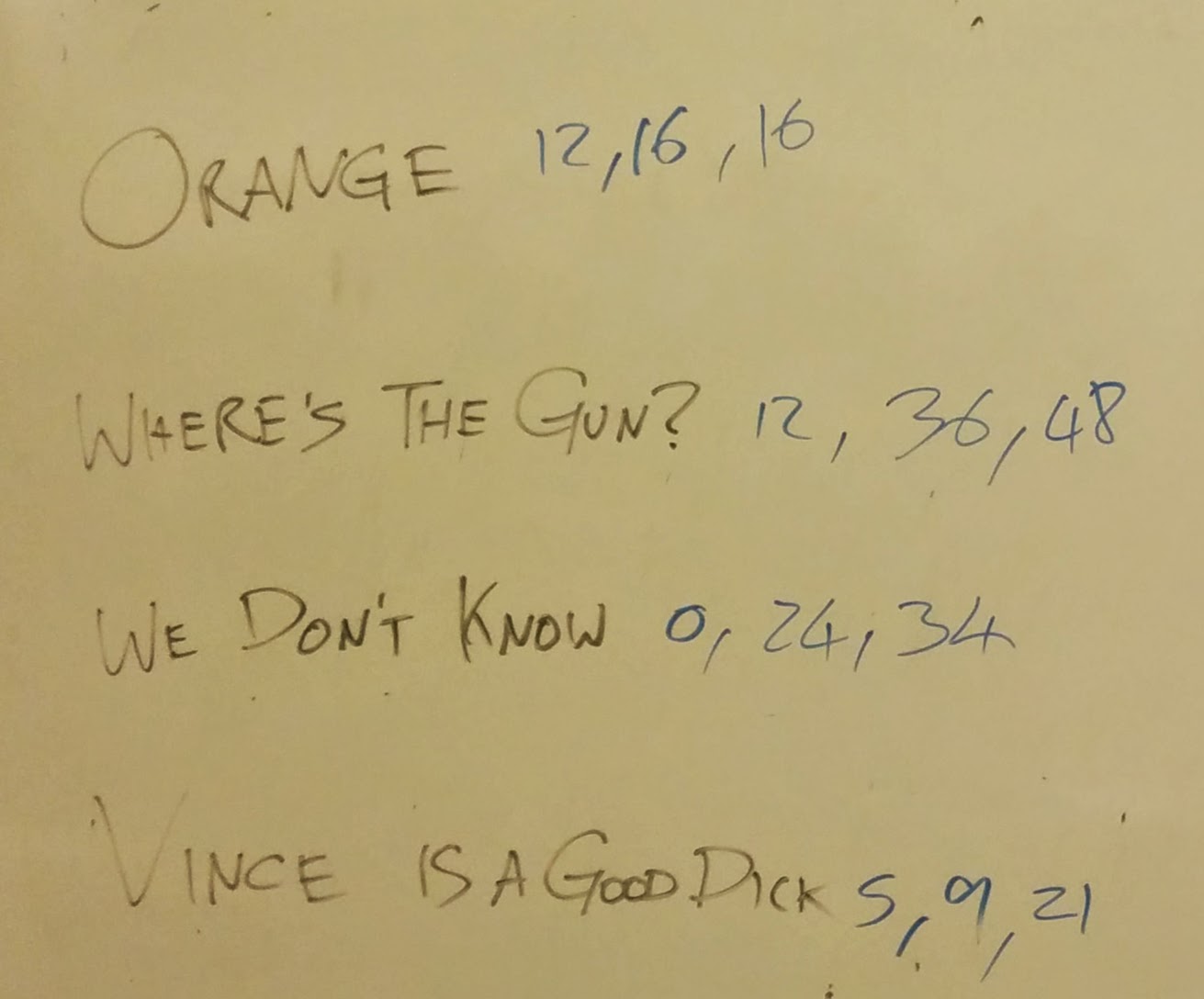
You can see the various duels here:

As you can see, very little cooperation happened this way and in fact because everyone could see what everyone else was doing Orange took advantage of the last round to create a coalition and win. We also see one particular duel that cost two teams very highly (because the ‘dice rolls’ did not really help).
After this I suggest to the class that we play again but that no one got to see what was happening to the other teams (this was actually suggested to me by students the year before). We went ahead with this and used \(delta=.25\): so the game had a less chance of carrying on.
You can see the result and duels here (this had to be squeezed on to a board that could be hidden):

Based on the theory we would expect more cooperation to be likely but as you can see this did not happen.
The tie at the end was settled with a game of Rock Paper Scissors Lizard Spock which actually gave place to a rematch of the Rock Paper Scissors Lizard Spock tournament we played earlier. Except this time Laura, lost her crown :)