Here is a blog post that mirrors this post from last year.

I will be using my blog to extend the class meetings my Game Theory class and I have.

After playing the 2/3rds of the average game (you can see a plot of the results from last year and this year in the comments of the intro chapter).

After this we moved on to normal form games, and in particular discussed the matching pennies game:

“Two players each show a coin with either ‘Heads’ or ‘Tails’ showing. If both coins match then the 1st player (the row player) wins, otherwise the 2nd player (the column player) wins.”

This can be described as:

If you’d like to read a description of what each number represents take a look at my blog post from last year.

I asked all the students to get in to pairs and play against each other, collecting all the results with forms that you can find at this github repo.

After this we changed the game slightly to look like this:

The main point of this is to make sure that everyone understands the normal form game convention (by breaking the symmetry) and also to make it slightly more interesting (the row player now has more to win/lose by playing Heads).

I played both games with S and recorded the results to demo what was happening:

This is not what this post is about: I’m going to analyse the data collected :)

Here’s a python script that contains the data as well as the matplotlib code to obtain the plot for the initial game.

The plot shows the probability with which players played ‘Heads’ as the rounds of the game played out:

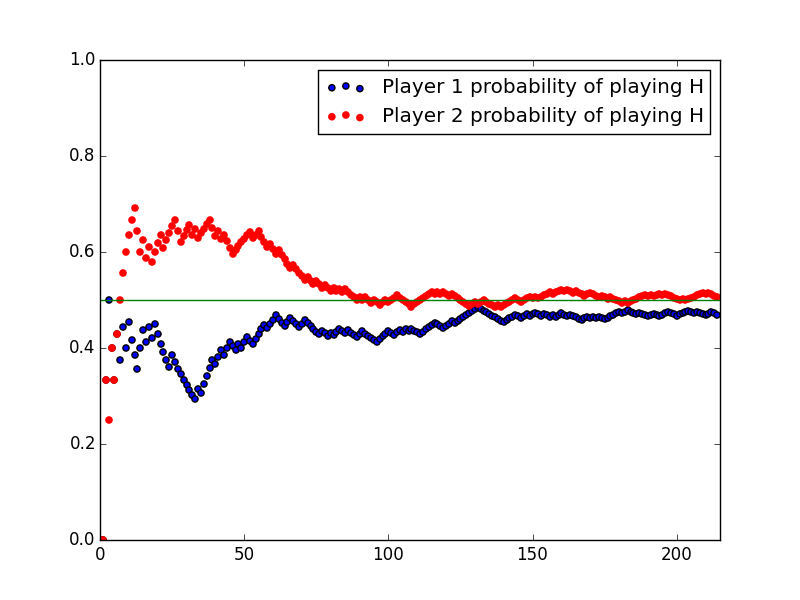
We see that we are very close at an overall probability of playing ‘Heads’ with probability 0.5. This is more or less what is expected. Now for something a bit more interesting.

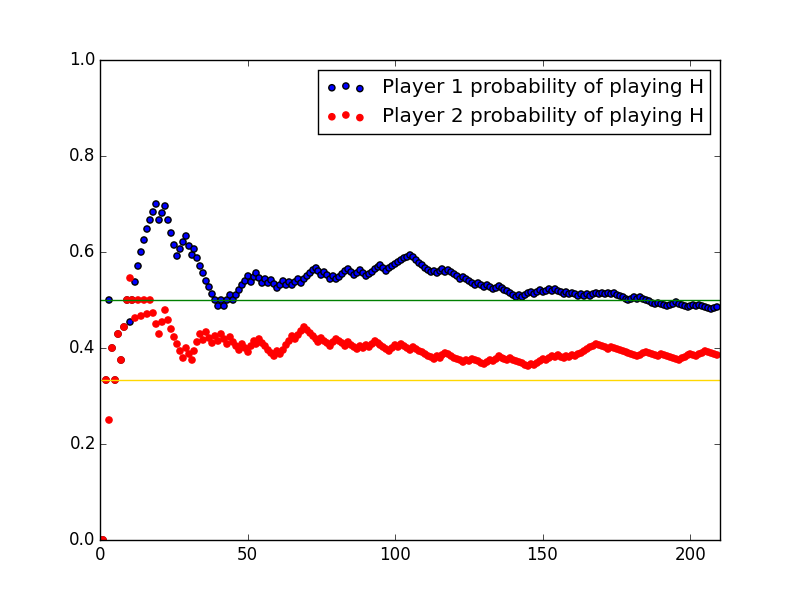
Here’s a python script that contains the data as well as the matplotlib code to obtain the plot for the modified game.

This is (just like last year) not quite what we expect (which is cool). It’s pretty late as I’m writing this and I need to head to sleep so I’ll point you towards the post from last year (here) and encourage you to read that and perhaps offer your own interpretation of what is happening :)

Finally: a big thanks to my students for engaging so much, I really appreciate it.