Here is my first post using jekyll, I’ll see how this goes and potentially migrate my blog completely to here.

This past year I’ve had a very minor role helping to organise the EURO Summer Institute for Healthcare. This took part from June 11 to 20 and it was really cool with 20 (ish) young academics (from first year PhD student to early years of Post Doc) coming together to present a paper they’re working on and get bespoke feedback from peers and an expert in the field.

The academic activities are really valuable but arguably of more value is the fact that everyone comes together and has a good time. One such ‘good time’ was a treasure hunt that because of some people dropping out of I was lucky enough to take part in. This was really great fun and in this post I’ll describe the problems as well as the Sage code my team used to almost win!

Here’s a photo that Paul Harper took of Pieter, Omar, Jenny and I huddled around Sage:

The treasure hunt involved us running around the small village to find an envelope with a particular mathematical problem. Once we’d solved that problem we would be given an indication as to where our next problem was.

Here are the various challenges (again: thanks to Paul for taking the photos!):

A clinical pathway problem (we did this one by hand):

A queueing problem:

To solve the above we wrote down the Markov chain (that’s actually the picture that Pieter is working on in the first photo of this blog post). Here’s the transition matrix corresponding to the Markov Chain:

\[\begin{pmatrix} -\frac{4_5}{45} & \frac{4}{45} & 0 & 0 & 0 \\
\frac{1}{20} & -\frac{5}{36} & \frac{1}{45} & \frac{1}{15} & 0 \\
0 & \frac{1}{10} & -\frac{1}{6} & 0 & \frac{1}{15} \\
0 & \frac{1}{20} & 0 & -\frac{13}{180} & \frac{1}{45} \\
0 & 0 & 0 & \frac{1}{10} & -\frac{1}{10} \end{pmatrix}\]

At the very beginning of the treasure hunt the organisers encouraged everyone to go and get their laptops. We originally thought that we’d manage without but at this point I ran to my room to go get my laptop :)

Here’s how we obtained the steady state probability \(\pi\):

Q = matrix([[-4/45,4/45,0,0,0,1],
            [1/20,-(1/20+3/45+1/45),1/45,3/45,0,1],
            [0,2/20,-(2/20+3/45),0,3/45,1],
            [0,1/20,0,-1/20-1/45,1/45,1],
            [0,0,0,2/20,-2/20,1]])
pi = Q.solve_left(vector([0,0,0,0,0,1]))

The above solves the matrix equation \(\pi Q=0\) with an extra column in \(Q\) to ensure that the elements of \(\pi\) sum to 1.

Finally, the particular questions asked for the following weighted sum (corresponding the mean utilisation):

pi[4]+2*pi[2]+1*pi[3]+1*pi[1])/2

This gave a value of about \(0.499\).

I’m obviously missing out a couple of details (the actually description of the state space) but I’ll leave that as an exercise.

A chinese postman problem:

I’m not entirely sure what we did here as Pieter kind of ran with this one but at some point I was asked to calculate a matching on our graph. Here’s the Sage code:

sage: K = 500  # The inbuilt matching algorithm aim to maximise: we wanted to minimise so I threw a large constant in...
sage: G = Graph( { 1: {2: -23+K, 5:-20+K, 8:-19+K},
....:              2: {1: -23+K, 3:-8+K, 5:-18+K},
....:              3: {2: -8+K, 4:-5+K, 5:-16+K},
....:              4: {3: -5+K, 5:-14+K, 7:-7+K, 10:-21+K},
....:              5: {1: -20+K, 2:-18+K, 3:-16+K, 4:-14+K, 6:-1+K},
....:              6: {5: -1+K, 7:-8+K, 8:-20+K, 9:-12+K, 10:-17+K},
....:              7: {4: -7+K, 6:-8+K},
....:              8: {1: -19+K, 6:-20+K, 9:-15+K, 11:-20+K},
....:              9: {6:-12+K, 8:-15+K, 10:-14+K, 11:-12+K},
....:              10: {4:-21+K, 6:-17+K, 9:-14+K, 11:-18+K},
....:              11: {8:-20+K, 9:-12+K, 10:-18+K},
....:               }, sparse = True)
sage: G.matching()
[(1, 8, 481), (2, 3, 492), (4, 7, 493), (5, 6, 499), (9, 11, 488)]

I’m not entirely sure that’s the right Graph I was supposed to use but it’s what I have left over in my Sage notebook…

A packing problem:

I had remembered seeing that packing problems were implemented in Sage so as we were running back from collecting the clue I yelled: this will take 3 minutes!

Sadly, this wasn’t the case as the only implementation involves bins of the same size (which isn’t the case here). As I read around the docs the rest of my team was able to solve this heuristically which left us with the last challenge and at this point nicely in the lead!

The problem of doom that made everyone cry:

After having pulled in the data here is about as far as Sage got us:

p = list_plot(healthy, color='red', size=30)
p += list_plot(pathological, color='green',size=30)
p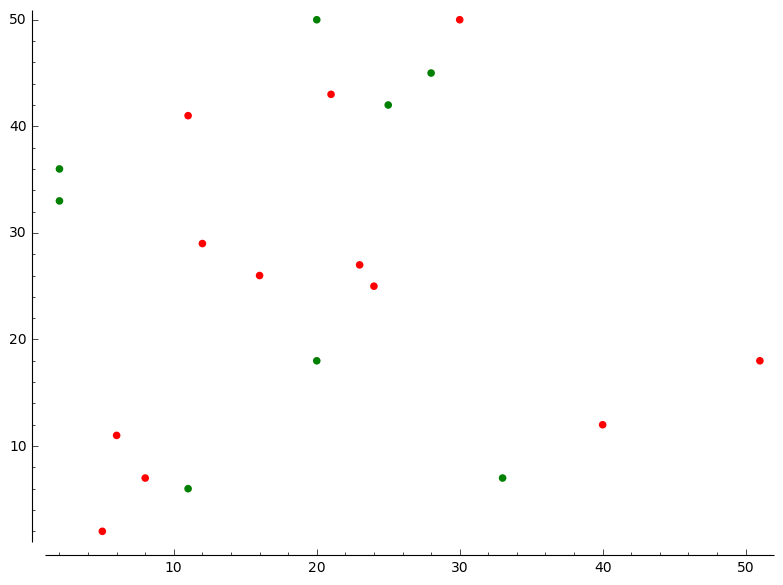

This was a tricky problem. We had no wifi in our hotel so downloading a relevant R package was out of the question.

We eventually formulated a non linear integer program but sadly our solver didn’t seem able to handle it in time. With two minutes to go (the deadline was dinner) one of the teams who had been doing things very steadily ran over claiming that they might have a solution. Everyone went quiet and walked over as their solution was checked and verified. It was a really nice moment as everyone clapped and cheered. Here’s a picture of a bunch of us crowded around the solution understanding how they took a stab at fixing some of the variables so that the solver could get the solution.

This was a phenomenal piece of fun. You can find another description with a bunch of funny photos of us all struggling here.

If anyone has some suggestions to how we could have solved any problems any faster I’d be delighted to hear them :)