Sophisticated IPD strategies beat simple ones
The Iterated prisoners dilemma (IPD) has been an active area of study since the 1980s following Robert Axelrod’s computer tournaments. With a team of over 50 contributors I am one of many who have built a Python library that allows for sustainable study of it: github.com/Axelrod-Python/Axelrod. This library is now coming of age and a number of research projects are making use of it. This blog post will describe two related pieces of work. Recent (2012) research as well as the results of Axelrod’s original tournaments have lead to a belief that simple strategies do just as well (if not better) than more complex ones. The two papers I’m going to describe show that’s not really true.
This is joint work with a number of talented people:
The two papers in question are:
- Evolution Reinforces Cooperation with the Emergence of Self-Recognition Mechanisms: an empirical study of the Moran process for the iterated Prisoner’s dilemma
- Reinforcement Learning Produces Dominant Strategies for the Iterated Prisoner’s Dilemma EDIT: Here is the published version: journals.plos.org/plosone/article?id=10.1371/journal.pone.0188046
Both of these papers look at using a family (referred to as archetypes in the second paper) of strategies and training them using reinforcement learning algorithms.
Reinforcement learning refers to a collection of algorithms that train a model by exploring a space of actions and evaluating consequences of those actions: good actions are typically chosen more often than bad actions as the algorithm is allowed to “walk through” the state space. The reinforcement learning algorithms we have use are genetic algorithms and particle swarm optimisation algorithms.
There are a number of strategy archetypes described in the second paper but here’s a diagrammatic representation of a particular type of one of them called a LookerUp strategy:
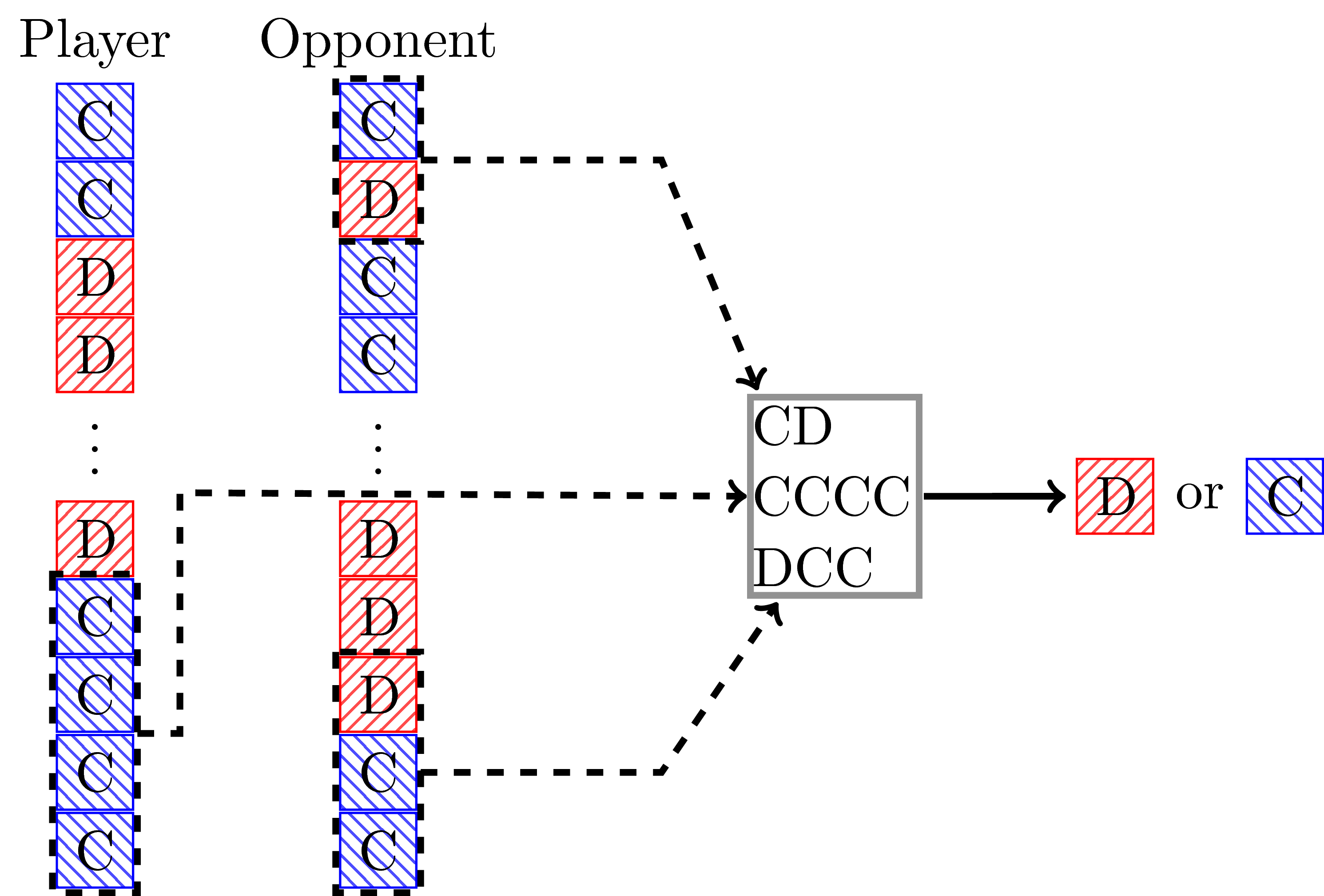
This strategy was first written about by Martin Jones: mojones.net/evolving-strategies-for-an-iterated-prisoners-dilemma-tournament.html.
The idea of that strategy is that it maps a given state of a history of recent plays and the early plays of the opponent to an action: whether to cooperate or defect.
The reinforcement learning algorithm (in this case a genetic algorithm) aims to learn what best mapping to use.
We do this for two settings:
- A Moran process: an evolutionary model of invasion and resistance across time during which high performing individuals are more likely to be replicated.
- A tournament: very similar to Axelrod’s famous tournaments of the 1980s.
This corresponds to the two papers.
In the first paper we observe a number of neat things:
- The trained strategies, with no input from us, evolve the ability to have a handshake: they recognise themselves. This seems particularly important in a Moran process of resisting invasion: where a single individual of another type is introduced.
- The size of the population is important. In a lot of theoretic work, Moran processes are only studied for \(N=2\) however we observe a boundary as to the performance of strategies across the case \(N=2\) and \(N>2\). This could have important ramifications from the point of view of theoretic studies.
In the second paper we consider not only a standard tournament with 200 turns but also a noisy tournament in which noise is injected. For the standard tournament the trained strategies outperform the designed ones. In the case of noise there is one particular strategy that has not seen much attention in the literature called “Desired Belief Strategy” that outperforms everything else (the trained strategies still do very well).
What’s interesting to note is that a family of strategies called Zero determinant strategies which have attracted a lot of recent interest due to the fact that they theoretically best any given individual do not do well in environments with complex opponents: Moran processes and/or large tournaments.
This is the largest numerical study of this type carried out (nothing comes close in terms of Moran processes) and I’ve only covered some of my personal highlights above. It would not have been possible without the Axelrod library which not only let us run the tournaments and Moran processes but also gives us access to a large strategy space (close to 200) with which our archetypes can be trained. It’s also been helpful to be able to Cardiff University’s hardware to run the numerous simulations.
The links above are on the arxiv pre print server and we are currently working to submit to leading journals.
EDIT: Here’s a link to a blog post Marc Harper wrote about the papers: marcharper.codes/2017-07-31/axelrod.html.