Last week my class and I looked at the basics of games with incomplete information. The main idea is that players do not necessarily know where there are in an extensive form game. We repeated a game I played last year that you can read about here.

Here is a picture of the game we played (for details take a look at the post from last year):

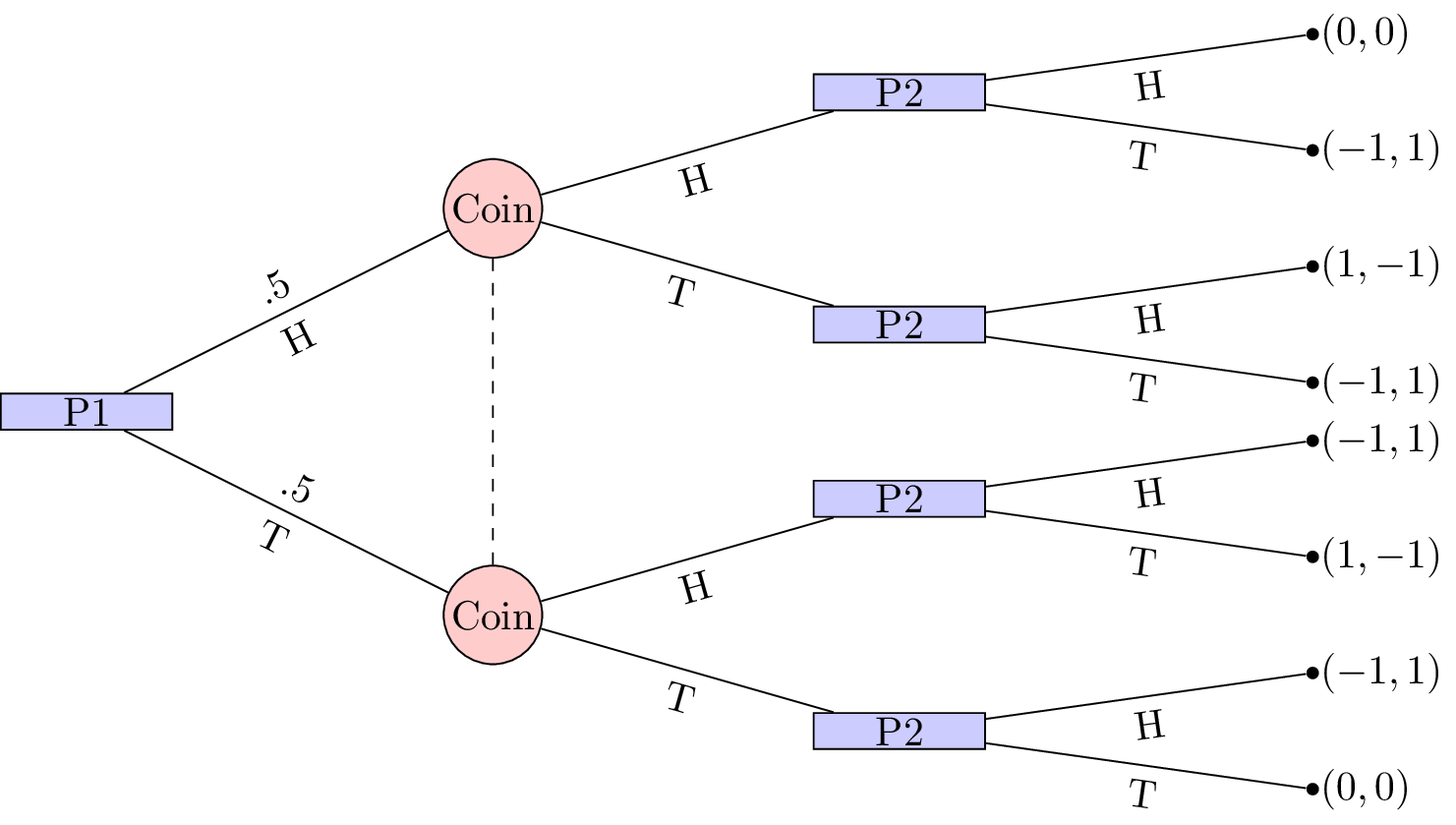
We played a round robing where everyone played against everyone else and you can see the results in these two notebook pages that Jason kept track off:

We see that the winner was Reg, who on both occasions of being the second player: went with the coin.

To find the Nash equilibria for this game we can translate it in to normal form game by doing the following two things:

  1. Identify the strategy sets for the players
  2. Averaging of the outcome probabilities

This gives the following strategies:

and

The strategies for the second player correspond to a 2-vector indexed by the information sets of the second player. In other words the first letter says what to do if the coin comes up as heads and the second letter says what to do if the coin comes up as tails:

  1. \(HH\): No matter what: play heads;
  2. \(HT\): If the coin comes up as heads: play heads. If the coin comes up as tails: play tails.
  3. \(TH\): If the coin comes up as heads: play tails. If the coin comes up as tails: play heads.
  4. \(TT\): No matter what: play tails;

Once we have done that and using the above ordering we can obtain the normal form game representation:

In class we obtained the Nash equilibria for this game by realising that the third column strategy (\(TH\): always disagree with the coin) was dominated and then carrying out some indifference analysis.

Here let us just throw it at Sage (here is a video showing and explaining some of the code):

The equilibria returned confirms what we did in class: the first player can more or less randomly (with bounds on the distribution) pick heads or tails but the second player should always agree with the coin.