A Sneak Preview of Game Theory in Sage (2/3): Matching Games
In my previous post here I described some of the Sage development that +James Campbell and I spent a lot of time this Summer working on. In that post I described some work that has subsequently been accepted and included in the latest release of Sage (here’s the latest changlog): code to calculate the Shapley value.
In this post I’ll talk about the second of 3 tickets that James and I worked on: looking at Matching games. This has not actually been reviewed yet so please do help us get this code in to Sage by taking a look at the ticket: 16331.
What is a matching game?
One of the best explanations of a matching game (also called the stable marriage problem) can be found in this video. That video really is awesome but it might be a bit long (it’s 25 minutes) so this very short video I threw together for a class I teach might be of interest (it is no where near as good as the previous one but it’s 3 minutes long).
Basically a matching game attempts to create links between two groups of people (referred to as suitors and reviewers) in such a way as no one wants to break their link:
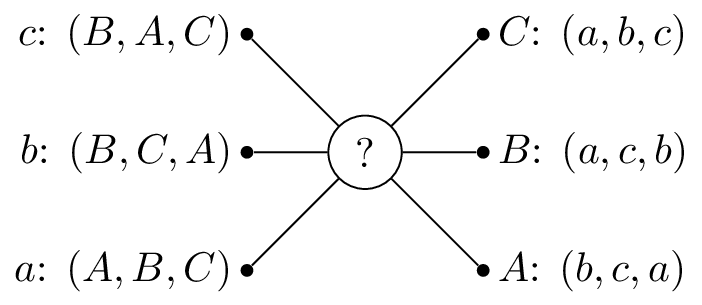
In the above picture we see the preferences of the suitors and the reviewers. So \(c\), prefers \(B\) to \(A\), and \(A\) to \(C\).
Here is the actual definition of a stable matching that I give my students:
A matching game of size \(N\) is defined by two disjoint sets \(S\) and \(R\) or suitors and reviewers of size \(N\). Associated to each element of \(S\) and \(R\) is a preference list:
A matching \(M\) is a any bijection between \(S\) and \(R\). If \(s\in S\) and \(r\in R\) are matched by \(M\) we denote:
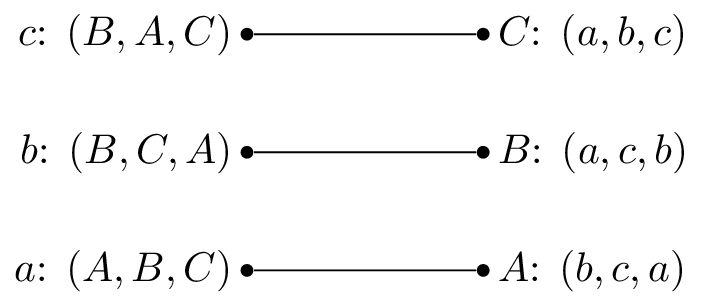
The above image defines a matching game, one possible matching could be given below:
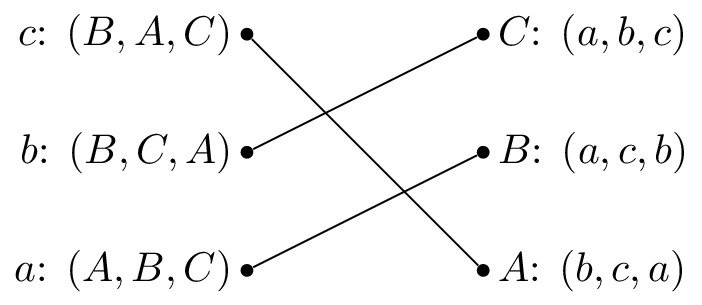
It’s immediate to note however that \(B\) and \(c\) prefer each other to their current matching: so the above matching is unstable. In that example \((B,c)\) is called a ‘blocking pair’.
Luckily Gale and Shapley obtained an algorithm that guarantees a stable matching and this is what James and I put together in to Sage.
First, let’s define a matching game:
sage: suitr_pref = {'a': ('B', 'A', 'C'),
....: 'b': ('B', 'C', 'A'),
....: 'c': ('A', 'B', 'C')}
sage: reviewr_pref = {'A': ('a', 'b', 'c'),
....: 'B': ('a', 'c', 'b'),
....: 'C': ('b', 'c', 'a')}
sage: m = MatchingGame([suitr_pref, reviewr_pref])You can see that python dictionaries are used for the functions \(f\) and \(g\) described above (the suitor preferences).
If you tab complete after typing m. you can see some of the methods and attributes associated with the MatchingGame class:
sage: m.
m.add_reviewer m.bi_partite m.db m.dumps m.rename m.reviewers m.solve m.version
m.add_suitor m.category m.dump m.plot m.reset_name m.save m.suitorsI won’t go in to much of the details of that year but you can get some help on anyone of those by typing ? after one of them (below you can see some of the output):
sage: m.solve?
Type: instancemethod
File: /Users/vince/sage/local/lib/python2.7/site-packages/sage/game_theory/matching_game.py
Definition: m.solve(self, invert=False)
Docstring:
Computes a stable matching for the game using the Gale-Shapley
algorithm.
...Let’s give that method a spin (as you can see it’ll use the Gale-Shapley algorithm).
sage: m.solve()
{'C': ['b'], 'a': ['B'], 'b': ['C'], 'A': ['c'], 'c': ['A'], 'B': ['a']}We see that a matching has been obtained. You can see the corresponding matching here:
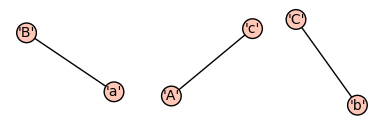
Another nice method that we implemented is to use the awesome graph theory stuff that’s in Sage so you can obtain the corresponding bi-partite graph:
sage: p = m.bi_partite()
Bipartite graph on 6 vertices
sage: p.show()You can see the corresponding plot here:
All of the above has not been reviewed yet so if you do have any comments they’d be very gratefully received. If you actually went over to trac and took a look at it there that would be great but otherwise just commenting here would be awesome.
This is the second in a series of 3 posts that I’ll get around to writing, in the next one I’ll cover ticket 16333: Normal Form Game. This is the biggest contribution by James as it involved interfacing with two other packages and also coding up a bespoke support enumeration algorithm.