Playing Games with Game Theory
Themes
reveal.js comes with a few themes built in:
Black (default) -
White -
League -
Sky -
Beige -
Simple
Serif -
Night -
Moon -
Solarized

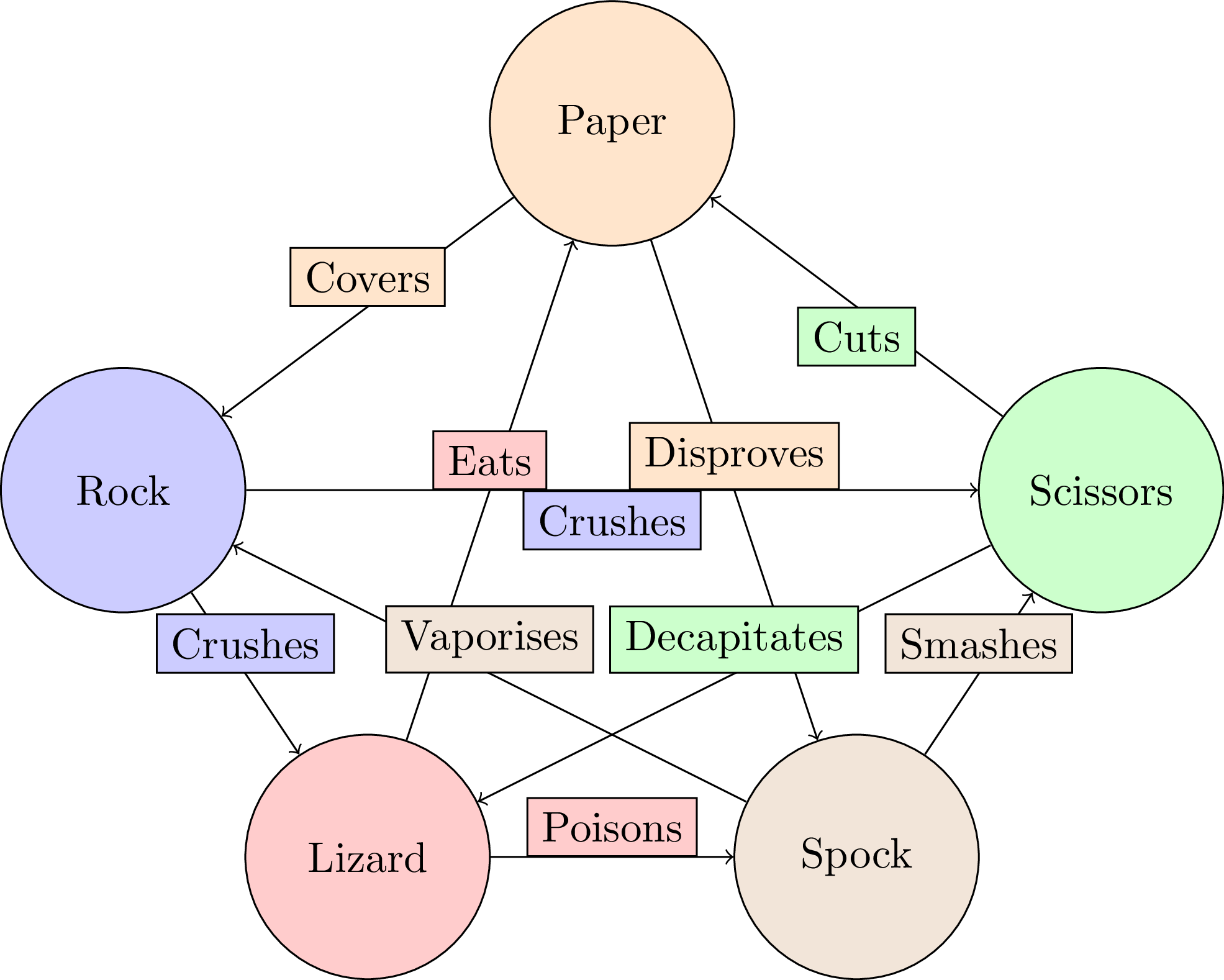
Tournament
Advice for foreigners on how Britons walk
“The British have little sense of pavement etiquette, preferring a slalom approach to pedestrian progress. When two strangers approach each other, it often results in the performance of a little gavotte as they double-guess in which direction the other will turn.”
Advice for foreigners on how Britons walk
“Telling people how to walk is simply not British.”
“But on the street? No, we don’t walk on the left or the right. We are British and wander where we will...”
import random
def walk(number_of_walks):
"""
Simulate people walking along the pavement
"""
reds = [random.choice('LR') for k in range(number_of_walks)]
blues = [random.choice('LR') for k in range(number_of_walks)]
bumps = sum([reds[k] != blues[k] for k in range(number_of_walks)])
return bumps
# Let us plot a large number of these interactions
num_of_walks = 500
num_of_reps = 2000
bins = 20
plt.hist([walk(num_of_walks) for k in range(num_of_reps)], bins=bins);
# What if everyone walks on the left?
def walk(number_of_walks):
"""
Simulate people walking along the pavement
"""
reds = [random.choice('L') for k in range(number_of_walks)]
blues = [random.choice('L') for k in range(number_of_walks)]
bumps = sum([reds[k] != blues[k] for k in range(number_of_walks)])
return bumps
plt.hist([walk(num_of_walks) for k in range(num_of_reps)], bins=bins);
# What if 1 person walks on the left and the other on the right?
def walk(number_of_walks):
"""
Simulate people walking along the pavement
"""
reds = [random.choice('L') for k in range(number_of_walks)]
blues = [random.choice('R') for k in range(number_of_walks)]
bumps = sum([reds[k] != blues[k] for k in range(number_of_walks)])
return bumps
plt.hist([walk(num_of_walks) for k in range(num_of_reps)], bins=bins);
# Evolutionary dynamics with a mutation rate:
size_of_population = 100 # Number of people
number_of_rounds = 500 # How many rounds
mutation_rate = .05 # Chance of changing strategy
death_rate = .05 # Chance of removal
reds = ['L' for k in range(size_of_population)]
blues = ['L' for k in range(size_of_population)]
red_data = [sum([k == 'L' for k in reds])]
blue_data = [sum([k == 'L' for k in reds])]
for rnd in range(number_of_rounds): # Loop through rounds
for j, pair in enumerate(zip(reds, blues)): # Loop through players
if random.random() < mutation_rate: # Check if random change
reds[j], blues[j] = random.choice('LR'), random.choice('LR')
if pair[0] != pair[1]: # If bump
if random.random() < death_rate: # If mind change
reds[j], blues[j] = blues[j], reds[j]
red_data.append(sum([k == 'L' for k in reds])) # Data collection
blue_data.append(sum([k == 'L' for k in blues]))
plt.plot(red_data);
plt.plot(blue_data);
Mathematics can help understand how behaviour emerges.
Golden Balls
TV show from Feb 2008 to Feb 2009 where a jackpot is to be shared between 2 contestants who secretly choose to "split" or "steal".
- If both players "split", the jackpot is split equally between them.
- If 1 player "splits" and the other "steals", the stealer gets the whole jackpot and the splitter leaves with nothing.
- If both players "steal", they both leave with nothing.
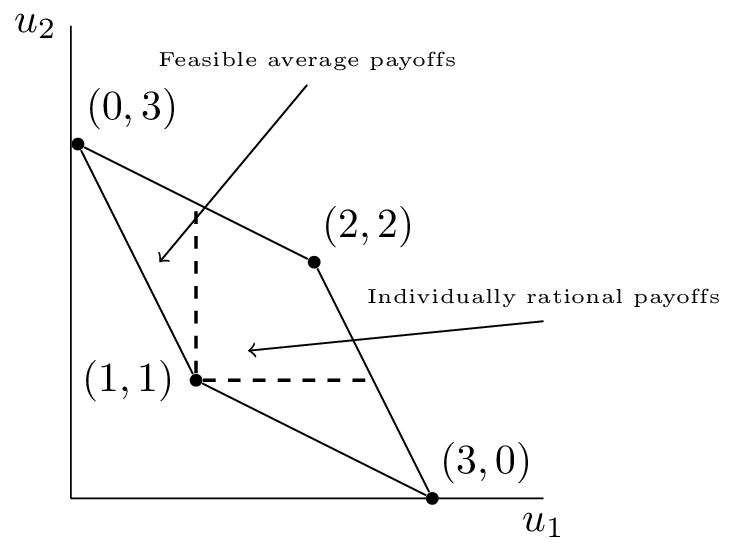
| Cooperate | Defect | |
| Cooperate | (3,3) | (0,5) |
| Defect | (5,0) | (1,1) |
Axelrod's computer tournament
Cooperator
Always cooperate.
Defector
Always defect.
Alternator
Start by cooperating and then switch.
Random
Play randomly.
Tit For Tat
Start by cooperating and then do whatever your opponent does in the previous round.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| Alternator | C | D | C | D | C | D | C | D |
| Tit For Tat | C | C | D | C | D | C | D | C |
| C | D | |
| C | (3,3) | (0,5) |
| D | (5,0) | (1,1) |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| Alternator | 3 | 5 | 0 | 5 | 0 | 5 | 0 | 5 |
| Tit For Tat | 3 | 0 | 5 | 0 | 5 | 0 | 5 | 0 |
| Alternator | Cooperator | Defector | Random | Tit For Tat | |
| Alternator | 2.0 | 4.0 | 0.5 | 2.3 | 2.5 |
| Cooperator | 1.5 | 3.0 | 0.0 | 1.5 | 3.0 |
| Defector | 3.0 | 5.0 | 1.0 | 3.0 | 1.0 |
| Random | 2.2 | 4.0 | 0.5 | 2.3 | 2.7 |
| Tit For Tat | 2.5 | 3.0 | 1.0 | 2.3 | 3.0 |
Demonstration
Applications of Game Theory
- Economics
- Biology
- Computer Science

(1928-2015)
Brouwer's fixed point theorem
