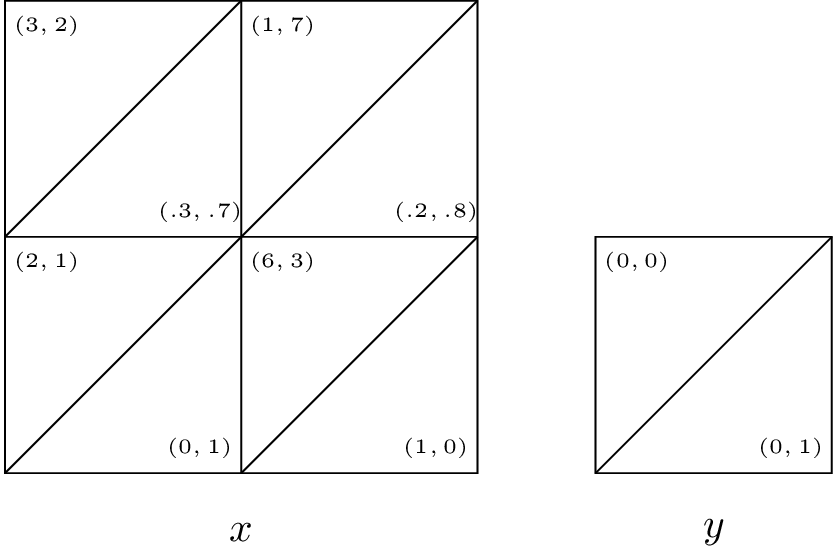
Consider the pairwise contest games with the following associated two player games:
\[\begin{pmatrix} (2,2)&(4,5)\\ (5,4)&(1,1)\\ \end{pmatrix}\]
\[\begin{pmatrix} (1,1)&(0,0)\\ (0,0)&(1,1) \end{pmatrix}\]
Identify all evolutionary stable strategies.
Consider the following game:
In a mathematics department, researchers can choose to use one of two systems for typesetting their research papers: LaTeX or Word. We will refer to these two strategies as \(L\) and \(W\) respectively. A user of \(W\) receives a basic utility of 1 and as \(L\) is more widely used by mathematicians out of the department and is in general considered to be a better system a user of \(L\) gets a basic utility of \(\alpha > 1\). Members of the mathematics department often collaborate and as such it is beneficial for the researchers to use the same typesetting system. If we let \(\mu\) represent the proportion of users of \(L\) we let:
\[u(L,\chi)=\alpha+2\mu\] \[u(W,\chi)=1+2(1-\mu)\]
What are the evolutionary stable strategies?
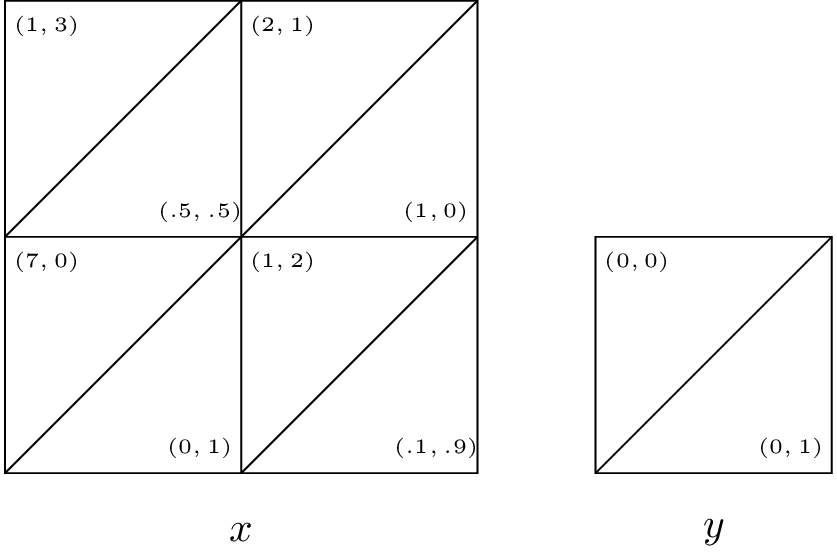
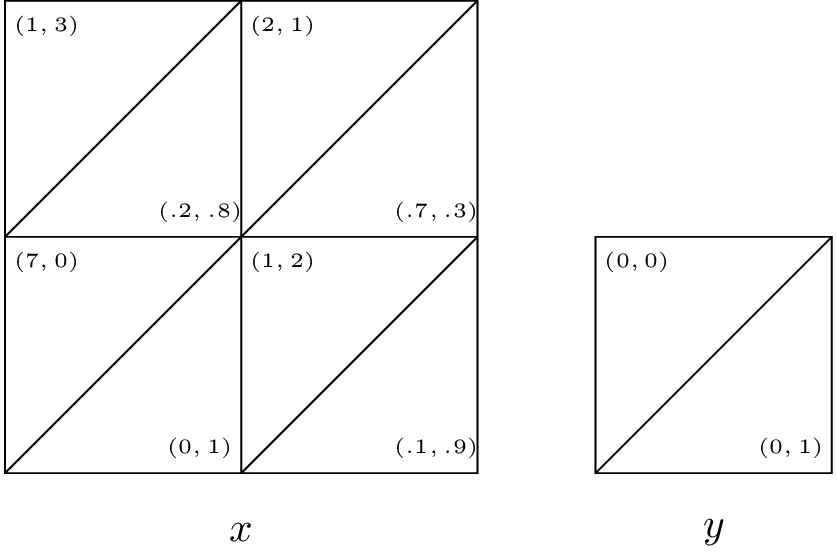
Consider the following two normal form games:
\[A=\begin{pmatrix} (3,0)&(-1,-1)&(1,2)\\ (1,0)&(-1,1)&(2,0)\\ \end{pmatrix}\]
\[B=\begin{pmatrix} (2,2)&(1,1)&(1,3)\\ (1,3)&(-2,-3)&(4,2)\\ \end{pmatrix}\]
Assume both players play either game \(A\) or game \(B\) with probability \(1/2\), neither player knows which game is played. Obtain the Nash equilibrium for this game.
Repeat the analysis of the principal agent game assuming that \(p\) is the probability of the project being successful in case of a high level of effort by the employee.
- What are the expected utilities to the employer and the employee?
- Obtain a condition for which the employer should offer a bonus.
Obtain the Markov Nash equilibrium (in pure strategies if it exists) for the following games assuming \(\delta=1/4\).
