Homework 4 Solution - Evolutionary games, games with incomplete information and stochastic games
-
Consider the pairwise contest games with the following associated two player games:
Solution
Using the Equality of payoffs theorem we obtain the Nash equilibria:
The two pure Nash equilibria are not ESS (because they are not symmetric).
for \(\sigma=(\omega,1-\omega)\):
and:
thus (after some algebraic manipulation):
which is positive for \(\omega \ne 1/2\) so this mixed strategy is an ESS.
Solution
Using the Equality of payoffs theorem we obtain the Nash equilibria:
The two pure Nash equilibria are ESS (because of the first condition of the theorem relating an evolutionary stable strategy to the Nash equilibrium of the associated game).
As before:
and:
so not an ESS.
Identify all evolutionary stable strategies.
-
Consider the following game:
In a mathematics department, researchers can choose to use one of two systems for typesetting their research papers: LaTeX or Word. We will refer to these two strategies as \(L\) and \(W\) respectively. A user of \(W\) receives a basic utility of 1 and as \(L\) is more widely used by mathematicians out of the department and is in general considered to be a better system a user of \(L\) gets a basic utility of \(\alpha > 1\). Members of the mathematics department often collaborate and as such it is beneficial for the researchers to use the same typesetting system. If we let \(\mu\) represent the proportion of users of \(L\) we let:
What are the evolutionary stable strategies?
Solutions
Using the theorem for necessity of stability we have the following candidate ESS:
- \(\sigma_L\): everyone uses \(L\), thus \(\mu=1\) (we have \(u(L,\chi)>u(W,\chi)\).
- \(\sigma_W\): everyone uses \(W\), thus \(\mu=0\) (we have \(u(L,\chi)<u(W,\chi)\).
- \(\sigma_m\): some use \(L\) and some use \(W\), by the theorem we have \(u(L,\chi)=u(W,\chi)\) which implies \(\alpha+2\mu=1+2(1-\mu)\) giving \(\mu=\frac{3-\alpha}{4}\).
Now we consider the post entry population \(\chi_\epsilon=(1-\epsilon)\sigma^*+\epsilon\sigma\) (where \(\sigma^*\) is the base strategy and \(\sigma\) is the entry population). We denote \(\sigma=(\mu,1-\mu)\) and \(\sigma^*=(\mu^*,1-\mu^*)\) and \(\delta = u(\sigma^*,\chi_\epsilon)-u(\sigma,\chi_\epsilon)\). We have:
which gives:
We now consider each potential ESS in turn, if \(\delta>0\) for all \(\epsilon<\bar\epsilon\) for some \(\bar\epsilon\) then we have an ESS (this is by definition):
- \(\mu^*=1\): \(\delta=(1-\mu)(1+\alpha+4\epsilon(\mu-1))>(1-\mu)(1+\alpha-4\epsilon)>0\) for all \(\mu\ne1\) and \(\epsilon<\bar\epsilon=\frac{1+\alpha}{4}\). Thus \(\sigma_L\) is an ESS.
- \(\mu^*=0\): \(\delta=-\mu(\alpha - 3+4\epsilon\mu)\). If \(\alpha\geq 3\) then \(\delta \leq 0\) for all values of \(\mu, \epsilon\), thus if \(L\) is 3 times better than \(W\) \(\sigma_W\) is not an ESS. If \(\alpha<3\) \(\delta>0\) \(\Leftrightarrow\) \(\alpha-3+4\epsilon\mu<0\) \(\Rightarrow\) \(\alpha-3+4\epsilon\mu<\alpha-3+4\epsilon<0\) for all \(\mu\ne 0\) \(\epsilon<\bar\epsilon=\frac{3-\alpha}{4}\). Thus \(\sigma_W\) is an ESS for \(\alpha<3\).
- \(\mu^*=\frac{3-\alpha}{4}\): \(\delta=-4\epsilon\left(\frac{3-\alpha}{4}-\mu\right)^2<0\) for all \(\mu\ne\frac{3-\alpha}{4}\) and for all \(\epsilon>0\) so \(\sigma_m\) is not an ESS.
-
Consider the following two normal form games:
Assume both players play either game \(A\) or game \(B\) with probability \(1/2\), neither player knows which game is played. Obtain the Nash equilibrium for this game.
Solution
The described game is akin to the following game:
We see that \(s_2\) is dominated and solve the game using the equality of payoffs theorem to give the following Nash equilibrium:
-
Repeat the analysis of the principal agent game assuming that \(p\) is the probability of the project being successful in case of a high level of effort by the employee.
i. What are the expected utilities to the employer and the employee?
Solution
Repeating the analysis, we see that the employee will carry out a high effort iff:
Following the same argument as in the notes we arrive at:
thus:
The utilities are then:
Employer: Employee:
ii. Obtain a condition for which the employer should offer a bonus.
Solution
If no bonus is offered the employee has no incentive for a high effort thus \(\kappa=\omega=1\), thus the employer should offer a bonus iff:
-
Obtain the Markov Nash equilibrium (in pure strategies if it exists) for the following games assuming \(\delta=1/4\).
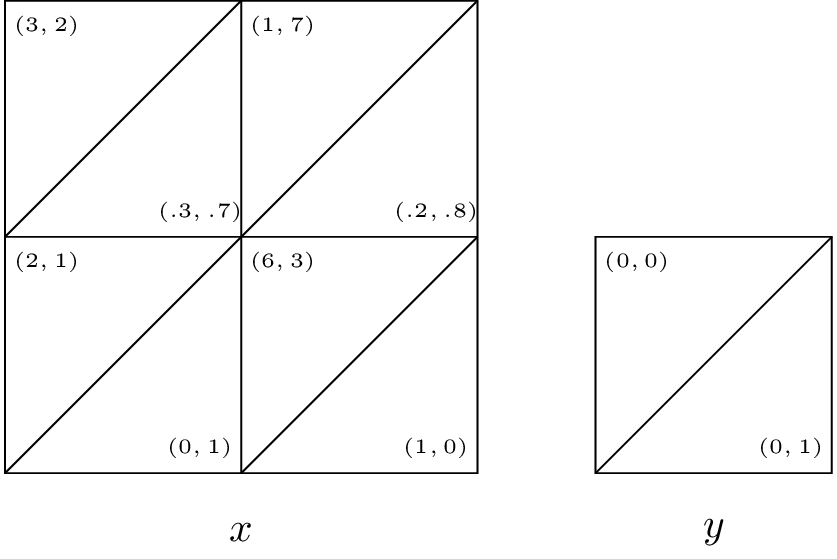
Solution
State \(y\) gives no value to either player so we only need to consider state \(x\). Let the future gains to player 1 in state \(x\) be \(u\) and the future gains to player 2 in state \(x\) be \(v\). Thus the players are facing the following game:
There are four possible equilibria:
-
\((a,c)\) which requires: \(3+3u/40\geq 2\) and \(2+3v/40\geq 7+v/20\) \(\Rightarrow\) \(u\geq -40/3\) and \(v\geq 200\). However if this is the equilibria then \(u=120/37\) and \(v=80/37\) which contradicts the constraints.
-
\((a,d)\) which requires: \(1+u/20\geq 6+u/4\) and \(2+3v/40\leq 7+v/20\) \(\Rightarrow\) \(u\leq -25\) and \(v\leq 200\). However if this is the equilibria then \(u=20/19\) and \(v=140/19\) which contradicts the constraints.
-
\((b,c)\) which requires: \(2\geq 3+3u/40\) and \(1\geq 3+v/4\) \(\Rightarrow\) \(u\leq -40/3\) and \(v\leq -8\). However if this is the equilibria then \(u=2\) and \(v=1\) which contradicts the constraints.
-
\((b,d)\) which requires: \(6+u/4\geq 1+u/20\) and \(1\leq 3+v/4\) \(\Rightarrow\) \(u\geq -25\) and \(v\geq -8\). However if this is the equilibria then \(u=8\) and \(v=4\) which does not contradict the constraints.
Thus \((b,d)\) is the unique pure strategy equilibrium.
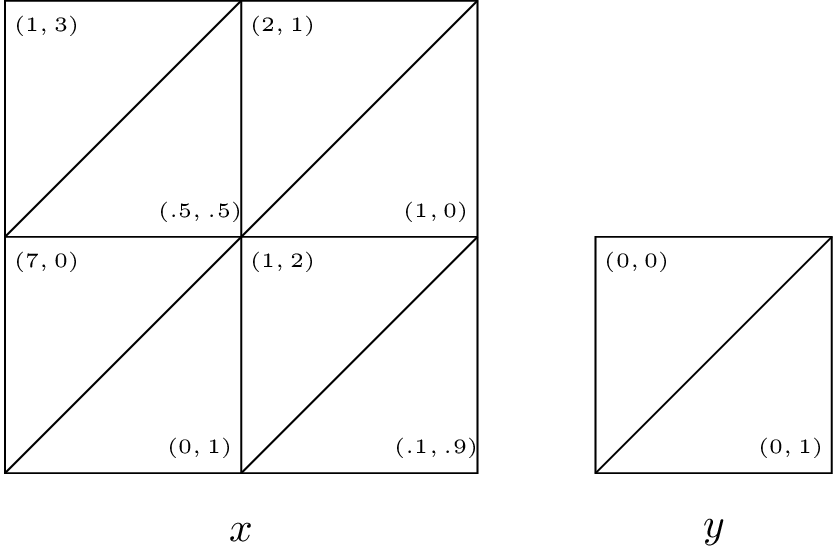
Solution
State \(y\) gives no value to either player so we only need to consider state \(x\). Let the future gains to player 1 in state \(x\) be \(u\) and the future gains to player 2 in state \(x\) be \(v\). Thus the players are facing the following game:
There are four possible equilibria:
-
\((a,c)\) which requires: \(1+u/8\geq 7\) and \(3+v/8\geq 1+v/4\) \(\Rightarrow\) \(u\geq 48\) and \(v\leq 16\). However if this is the equilibria then \(u=8/7\) and \(v=24/7\) which contradicts the constraints.
-
\((a,d)\) which requires: \(2+u/4\geq 1+u/40\) and \(3+v/8\leq 1+v/4\) \(\Rightarrow\) \(u\geq -40/9\) and \(v\geq 16\). However if this is the equilibria then \(u=8/3\) and \(v=4/3\) which contradicts the constraints.
-
\((b,c)\) which requires: \(7\geq 1+u/8\) and \(0\geq 2+v/40\) \(\Rightarrow\) \(u\leq 48\) and \(v\leq -80\). However if this is the equilibria then \(u=7\) and \(v=0\) which contradicts the constraints.
-
\((a,d)\) which requires: \(2+u/4\leq 1+u/40\) and \(2+v/40\geq 0\) \(\Rightarrow\) \(u\leq -40/9\) and \(v\geq -80\). However if this is the equilibria then \(u=40/39\) and \(v=80/39\) which contradicts the constraints.
Thus no Nash equilibrium exists in pure strategies.
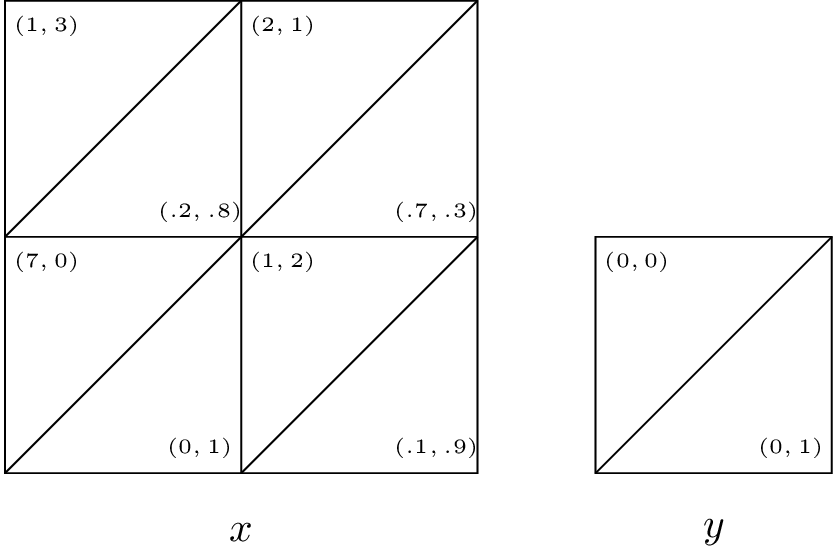
Solution
State \(y\) gives no value to either player so we only need to consider state \(x\). Let the future gains to player 1 in state \(x\) be \(u\) and the future gains to player 2 in state \(x\) be \(v\). Thus the players are facing the following game:
There are four possible equilibria:
-
\((a,c)\) which requires: \(1+u/20\geq 7\) and \(3+v/20\geq 1+7v/40\) \(\Rightarrow\) \(u\geq 120\) and \(v\leq 16\). However if this is the equilibria then \(u=20/19\) and \(v=60/19\) which contradicts the constraints.
-
\((a,d)\) which requires: \(2+7u/40\geq 1+u/40\) and \(1+7v/40\geq 3+v/20\) \(\Rightarrow\) \(u\geq -20/3\) and \(v\geq 16\). However if this is the equilibria then \(u=80/33\) and \(v=40/33\) which contradicts the constraints.
-
\((b,c)\) which requires: \(7\geq 1+u/20\) and \(0\geq 2+1v/40\) \(\Rightarrow\) \(u\leq 120\) and \(v\leq -80\). However if this is the equilibria then \(u=7\) and \(v=0\) which contradicts the constraints.
-
\((b,d)\) which requires: \(2+7u/40\leq 1+u/40\) and \(2+v/40\geq 0\) \(\Rightarrow\) \(u\leq -20/3\) and \(v\geq -80\). However if this is the equilibria then \(u=40/39\) and \(v=80/39\) which contradicts the constraints.
Thus no Nash equilibrium exists in pure strategies.
-