- Summarise the overall performance of the class (including the performance on the individual coursework);
- Summarise the performance of the class on the group coursework
Note that at this point in time the marks are provisional and could be scaled by the Exam board. I do not expect this to happen as the marks distributions are within a reasonable range of the University guidelines (TLDR: they are slightly higher than the norm).
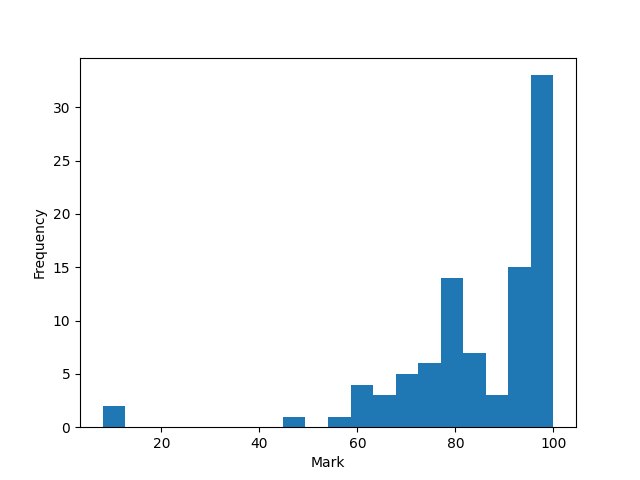
Overall class performance
A summary of the overall class performance is given here:
The University guidelines
The group coursework is a difficult assessment marked on a difficult scale. Summary of the class marks are here:
count 82
mean 66.54
std 10.08
min 37
25% 59.65
50% 67.20
75% 71.80
max 88
The average is a bit above the University guidelines which are that the mean class mark should be within \(62 \pm \frac{80}{\sqrt{n}}\) where \(n\) is 82 in this class (the number of students in the class).
Group class performance
I was incredibly impressed with the work you accomplished this Semester. Some projects where really innovative and well executed.
A summary of the class marks are here:
count 82
mean 53.78
std 10.56
min 35.00
25% 47.00
50% 50.00
75% 55.00
max 80
This is similar to the marks from last year where the median was 53.
Thank you again for your work this year. If you would like to discuss your marks and/or get further feedback please do get in touch.
]]>