Homework 2 Solution - Nash equilibrium in normal form games

Compute the Nash equilibrium (if they exist) in pure strategies for the following games:

Solution
$\begin{pmatrix} (5,\underline{3})&(70,-1)&(\underline{4},2)\\ (\underline{6},\underline{7})&(\underline{71},2)&(2,1) \end{pmatrix}$ $\begin{pmatrix} (\underline{6},\underline{7})&(2,1)&(\underline{4},6)\\ (0,4)&(\underline{3},\underline{8})&(2,3)\\ (1,2)&(1,\underline{5})&(1,1)\\ \end{pmatrix}$ $\begin{pmatrix} (\underline{\pi},\underline{e})&(1-\pi,\sqrt(e))\\ (\sqrt(2),1/e)&(\underline{2},\underline{1}) \end{pmatrix}$
For what values of $\alpha$ does a Nash equilibrium exist in pure strategies for the following game:

Solution
- $(r_1,c_1)$ is a pure strategy Nash equilibrium if:
  
  $3\geq 4\alpha$ and $5\geq\alpha$
  
  Thus $(r_1,c_1)$ is a Nash equilibrium iff $\alpha\leq3/4$.
- $(r_1,c_2)$ is a pure strategy Nash equilibrium if:
  
  $2-\alpha \geq \alpha$ and $\alpha\geq 5$
  
  This is not possible.
- $(r_2,c_1)$ is a pure strategy Nash equilibrium if:
  
  $4\alpha \geq 3$ and $6\geq \alpha^2$
  
  Thus $(r_2,c_1)$ is a Nash equilibrium iff $3/4\leq \alpha \leq \sqrt{6}$
- $(r_2,c_2)$ is a pure strategy Nash equilibrium if:
  
  $\alpha\geq 2-\alpha$ and $6\leq \alpha^2$
  
  Thus $(r_2,c_2)$ is a Nash equilibrium iff $\alpha\geq\sqrt{6}$
Consider the following game:

Suppose two vendors (of an identical product) must choose their location along a busy street. It is anticipated that their profit is directly related to their position on the street.

If we allow their positions to be represented by a points $x_1, x_2$ on the $[0,1]_{\mathbb{R}}$ line segment then we have:

$u_1(x_1,x_2)=\begin{cases}1/2,&\text{if }x_1=x_2\\ x_1+(x_2-x_1)/2,&\text{if }x_1< x_2\\ 1-x_1+(x_1-x_2)/2,&\text{otherwise} \end{cases}$ and $u_2(x_1,x_2)=\begin{cases}1/2,&\text{if }x_1=x_2\\ x_2+(x_1-x_2)/2,&\text{if }x_2< x_1\\ 1-x_2+(x_2-x_1)/2,&\text{otherwise} \end{cases}$

By considering best responses of each player, identify the Nash equilibrium for the game.

Solution

Without loss of generality, consider player 1’s best response. Consider $x_2<1/2$, if $x_1=x_2$ then $u_1(x_1,x_2)=1/2$. However $u_1(x_2+\epsilon,x_2)=1-x_2-\epsilon/2=1/2+1/2-x_2-\epsilon/2>1/2$ for some (arbitrarily) small $\epsilon>0$ . Thus for arbitrarily small $\epsilon$, $ x_1^*=x_2+\epsilon $. If $x_2>1/2$ a similar argument gives $x_1^*=x_2-\epsilon$. If $x_2=1/2$, considering $x_1=x_1$ we see that neither player has an incentive to move.

Thus we conclude:
$x_i^*=\begin{cases} x_j+\epsilon,&\text{ if }x_j<1/2\\ x_j-\epsilon&\text{ if }x_j>1/2\\ x_j&\text{ if }x_j=1/2\\ \end{cases}$
So the Nash equilibrium for this problem is $(\tilde x_1, \tilde x_2)=(1/2,1/2)$.
Consider the following game:
$\begin{pmatrix} (3,2)&(6,5)\\ (1,4)&(2,3) \end{pmatrix}$
Plot the expected utilities for each player against mixed strategies and use this to obtain the Nash Equilibria.

Solution

We have:
$u_1(r_1,(y,1-y))=3y+6-6y=6-3y$ $u_1(r_2,(y,1-y))=y+2-2y=2-y$
Here is a plot of this:

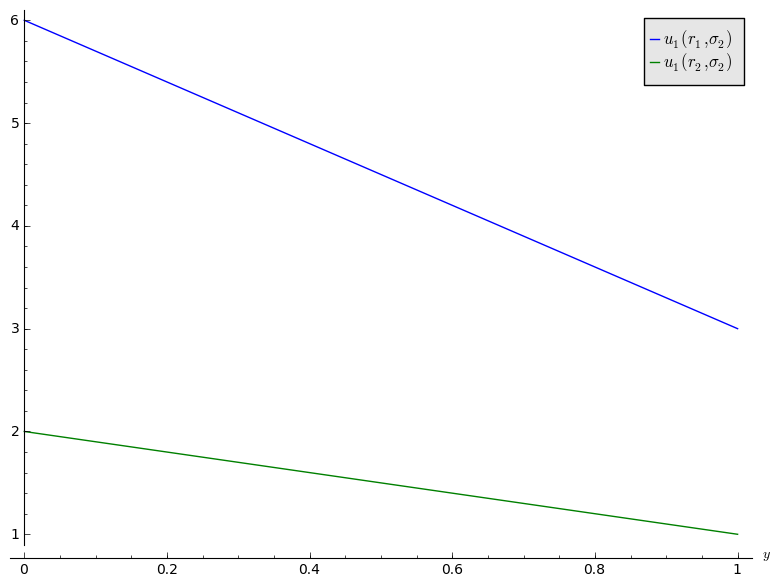
We see that $r_2$ is dominated by $r_1$. For player 2, we have:
$u_2((x,1-x),s_1)=2x+4-4x=4-2x$ $u_2((x,1-x),s_2)=5x+3-3x=3+2x$
Here is a plot of this:

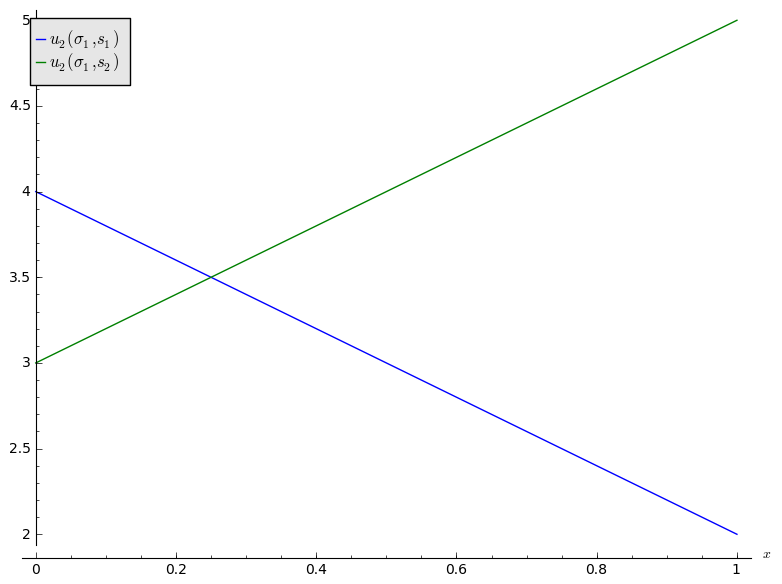
As $r_2$ is dominated, we see from the plot that the Nash equilibrium is $(r_1, c_2)$.
Assume a soccer player (player 1) is taking a penalty kick and has the option of shooting left or right: $S_1=\{\text{SL},\text{SR}\}$. A goalie (player 2) can either dive left or right: $S_2=\{\text{DL}, \text{DR}\}$. The chances of a goal being scored are given below:
1. Assume the utility to player 1 if the probability of scoring and the utility to player 2 the probability of a goal not being scored. What is the Nash equilibrium for this game?
Solution

We see that this is a zero sum game with bi-matrix:

There are no pure Nash equilibria. To obtain the NE, we use the Equality of Payoffs theorem:

$.2x+.8(1-x)=(.85x+.05(1-x))\Rightarrow x=15/28$ $.8y+.15(1-y)=.2y+.95(1-y)\Rightarrow y=4/7$

So the Nash Equilibrium is ${(15/28,13/28),(4/7,3/7)}$.
1. Assume that player 1 now has a further strategy available: to shoot in the middle: $S_1=\{\text{SL},\text{SM}, \text{SR}\}$ the probabilities of a goal being scored are now given:
Obtain the new Nash equilibrium for the game.

Solution

There are various approaches to this game, one is to apply the equality of payoffs theorem to all possible supports. Another is to plot the utilities:

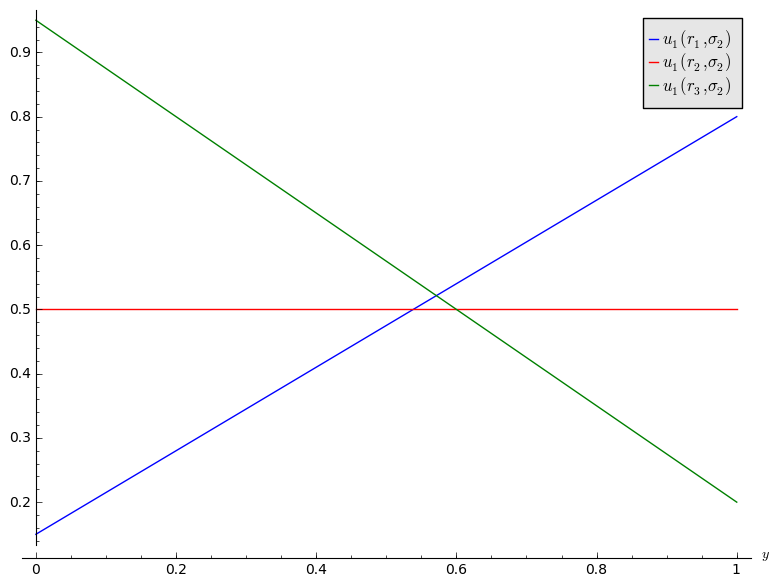
We see that $B_1=\{r_1,r_3\}$, by the equality theorem this gives $UD_1=\{r_1,r_3\}$ and so the Nash equilibria is the same as before.
In the notes the following theorem is given:

Every normal form game with a finite number of pure strategies for each player, has at least one Nash equilibrium.

Prove the theorem for 2 player games with $|S_1|=|S_2|=2$. I.e. prove the above result in the special case of $2\times 2$ games.

Solution

Let us consider the $2\times 2$ game:

There is no pure strategy Nash equilibrium if either:
1. $a_{11}<a_{21}$ and $b_{21}<b_{22}$ and $a_{22}<a_{12}$ and $b_{12}<b_{11}$ or
2. $a_{11}>a_{21}$ and $b_{21}>b_{22}$ and $a_{22}>a_{12}$ and $b_{12}>b_{11}$ or
In each of these cases we use the Equality of payoffs theorem:

which gives:

Similarly:

In both cases the $0<x,y<1$ as required.