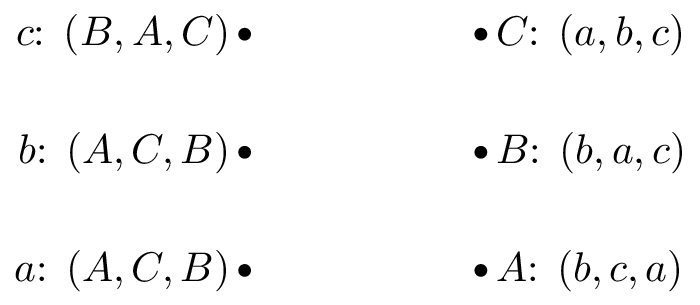
Obtain stable suitor optimal and reviewer optimal matchings for the matching games shown.
Game 1:
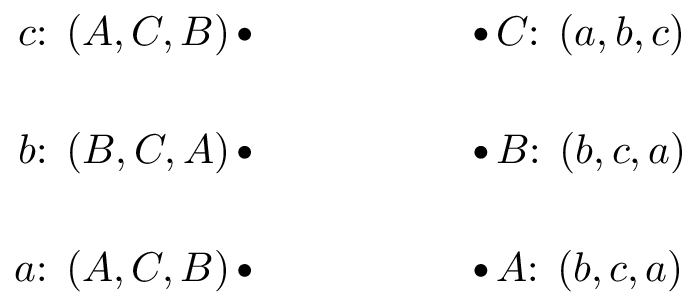
Game 2:
Game 3:
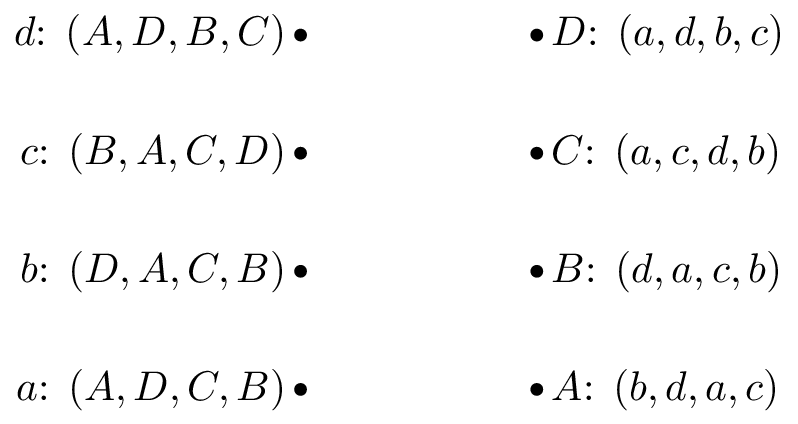
Game 4:
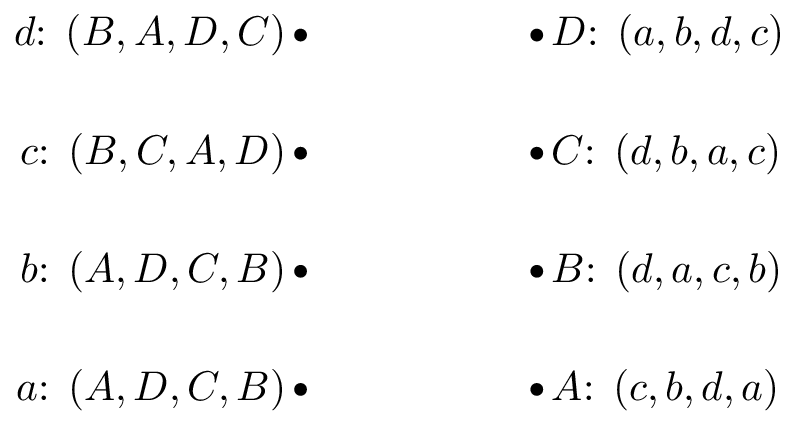
Consider a matching game where all reviewers have the same preference list. Prove that there is a single stable matching.
For the following cooperative games:
- Verify if the game is monotonic.
- Verify if the game is super additive.
- Obtain the Shapley value.
\[ v_1(C)=\begin{cases} 5,&\text{if }C=\{1\}\\ 3,&\text{if }C=\{2\}\\ 2,&\text{if }C=\{3\}\\ 12,&\text{if }C=\{1,2\}\\ 5,&\text{if }C=\{1,3\}\\ 4,&\text{if }C=\{2,3\}\\ 13,&\text{if }C=\{1,2,3\}\\ \end{cases} \]
\[ v_2(C)=\begin{cases} 6,&\text{if }C=\{1\}\\ 0,&\text{if }C=\{2\}\\ 5,&\text{if }C=\{1,2\}\\ \end{cases} \]
\[ v_3(C)=\begin{cases} 6,&\text{if }C=\{1\}\\ 6,&\text{if }C=\{2\}\\ 13,&\text{if }C=\{3\}\\ 6,&\text{if }C=\{1,2\}\\ 13,&\text{if }C=\{1,3\}\\ 13,&\text{if }C=\{2,3\}\\ 26,&\text{if }C=\{1,2,3\}\\ \end{cases} \]
\[ v_4(C)=\begin{cases} 6,&\text{if }C=\{1\}\\ 7,&\text{if }C=\{2\}\\ 0,&\text{if }C=\{3\}\\ 8,&\text{if }C=\{4\}\\ 7,&\text{if }C=\{1,2\}\\ 6,&\text{if }C=\{1,3\}\\ 12,&\text{if }C=\{1,4\}\\ 7,&\text{if }C=\{2,3\}\\ 12,&\text{if }C=\{2,4\}\\ 8&\text{if }C=\{3,4\}\\ 7,&\text{if }C=\{1,2,3\}\\ 24,&\text{if }C=\{1,2,4\}\\ 12,&\text{if }C=\{1,3,4\}\\ 12,&\text{if }C=\{2,3,4\}\\ 25,&\text{if }C=\{1,2,3,4\}\\ \end{cases} \]
Prove that the Shapley value has the following properties:
- Efficiency
- Null player
- Symmetry
- Additivity
Note that this does not prove that the Shapley value is the only vector that has those properties (it in fact is though).
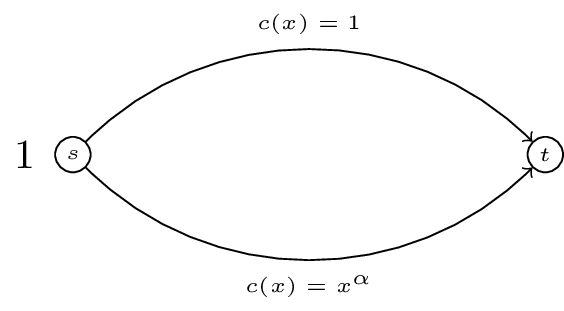
Calculate the Nash flow and the optimal flow for the following routing game:
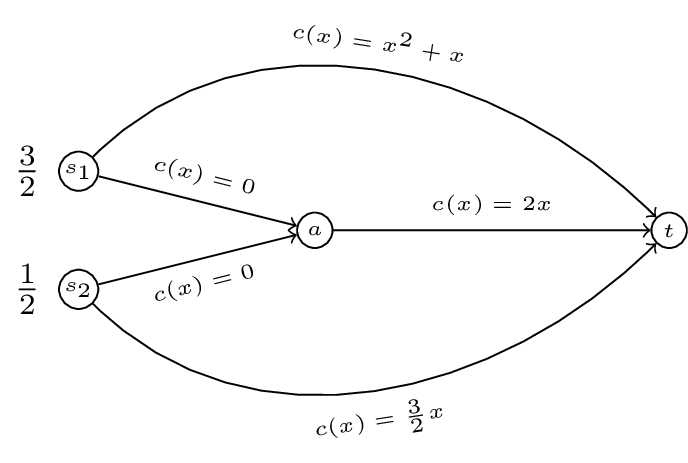
For a routing game the 'Price of Anarchy' is defined as:
\[\text{PoA}=\frac{C(\tilde f)}{C(f^*)}\]
For the game shown (a generalisation of "Pigou's example") obtain the PoA as a function of \(\alpha\).