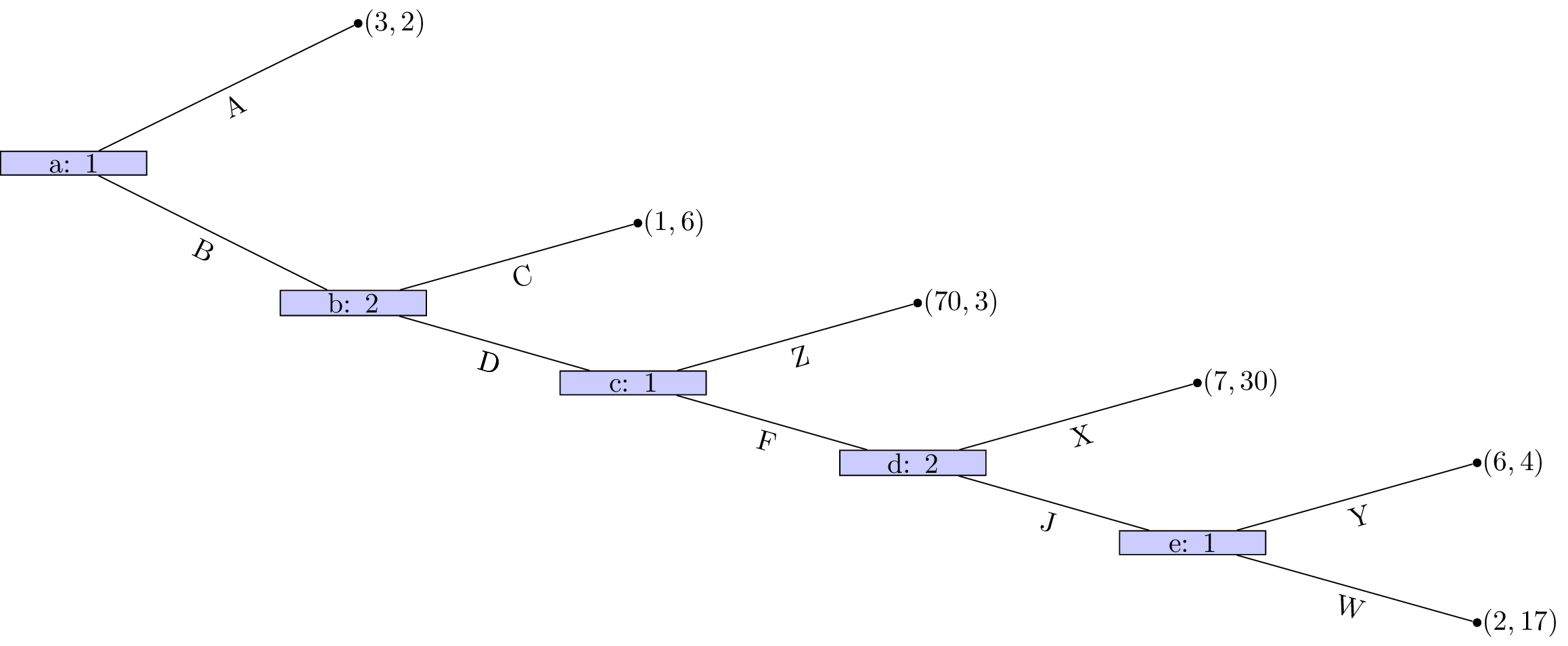
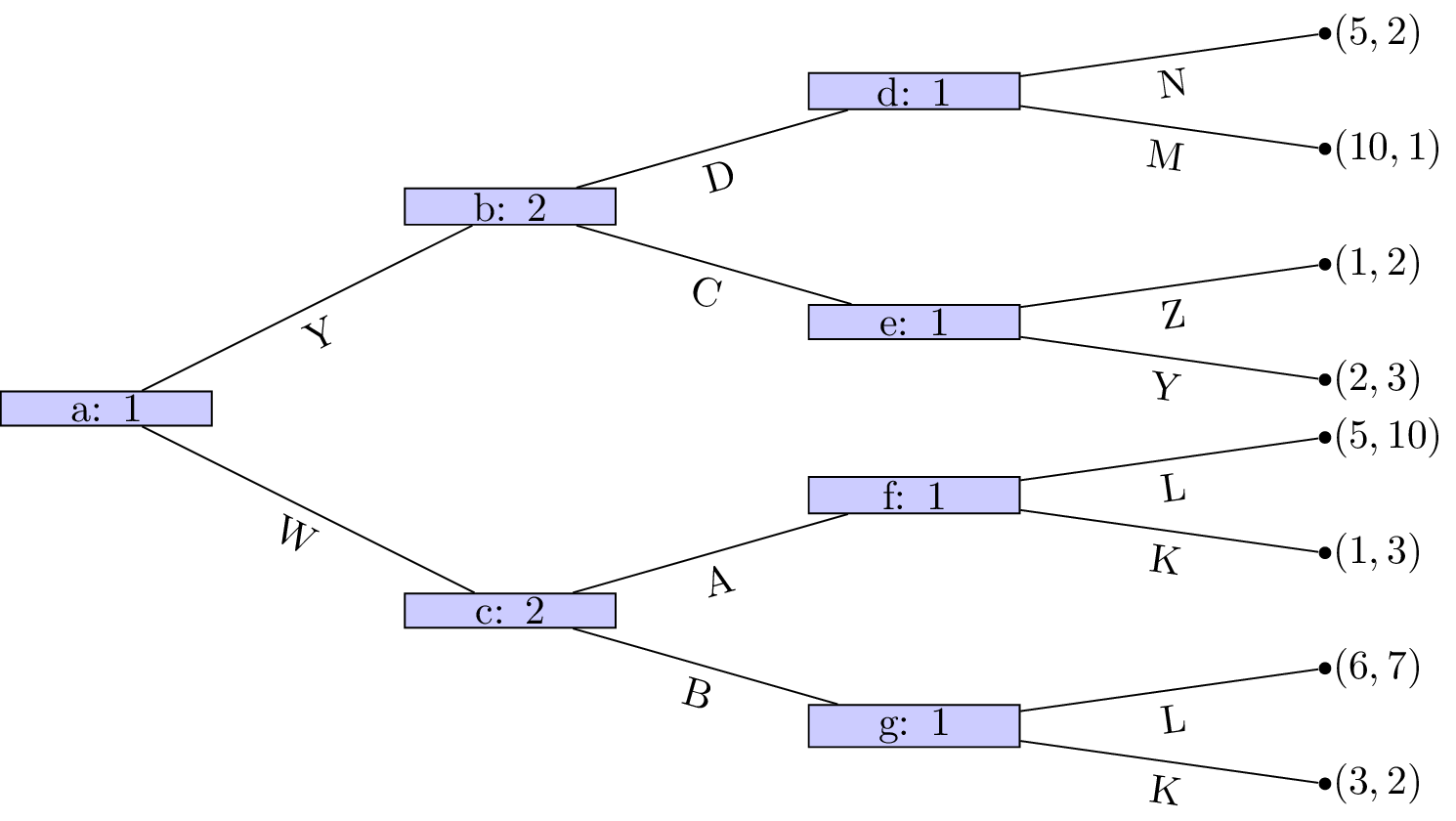
Obtain the Nash equilibrium for the following games using backward induction:
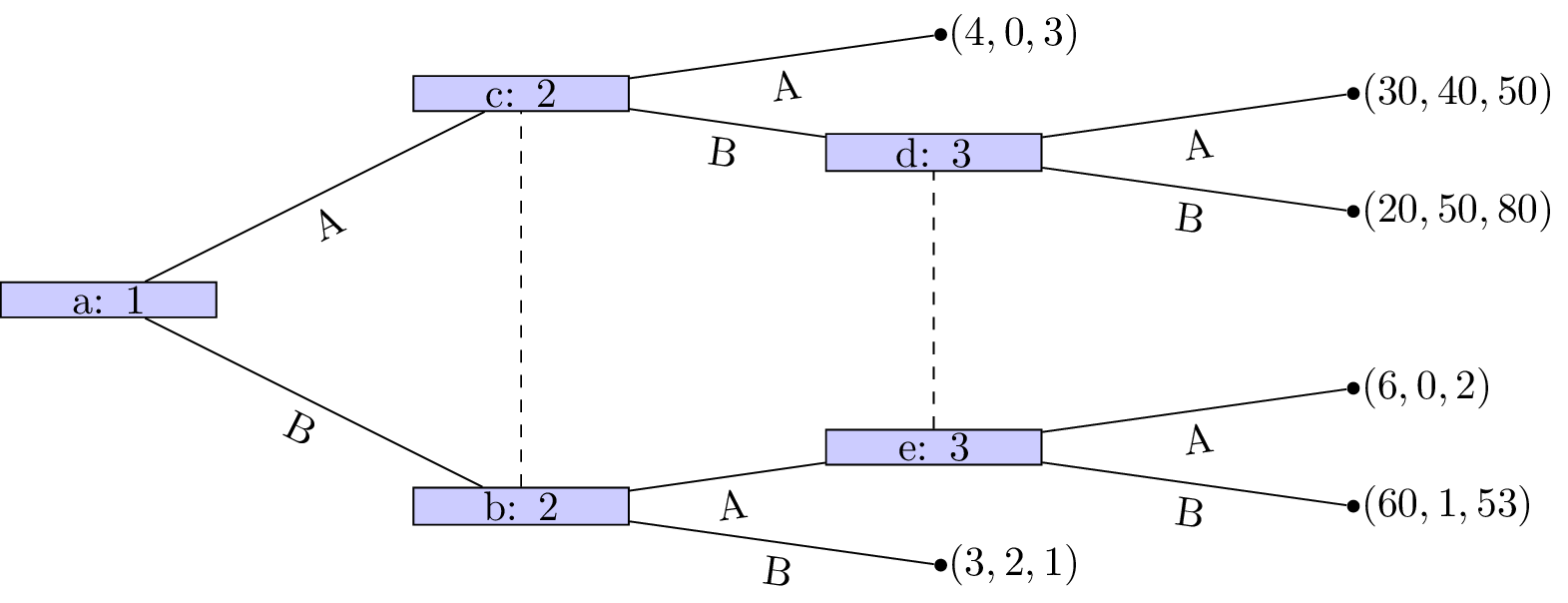
Obtain the Nash equilibrium for the following game:
Player 1 chooses a number \(x\geq 0\), which player 2 observes. After this simulataneously and independatly player 1 and player 2 choose \(y_1, y_2\in\mathbb{R}\) respectively. The utility to player 1 is given by \(2y_2y_1+xy_1-y_1^2-x^3/3\) and the utility to player 2 is given by \(-(y_1-2y_2)^2\).
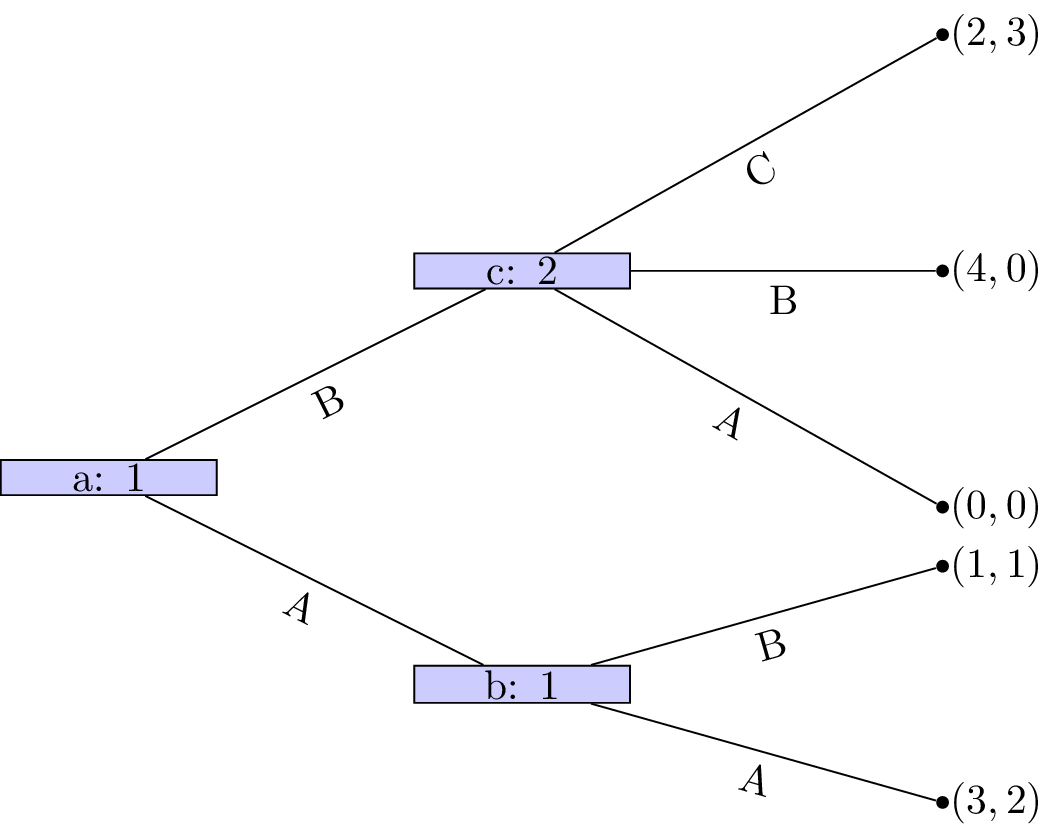
For each of the following games:
- Identify all subgames.
- Identify the corresponding normal form representations and hence obtain all Nash equilibrium.
- Identify which Nash equilibrium are also subgame perfect Nash equilibrium.
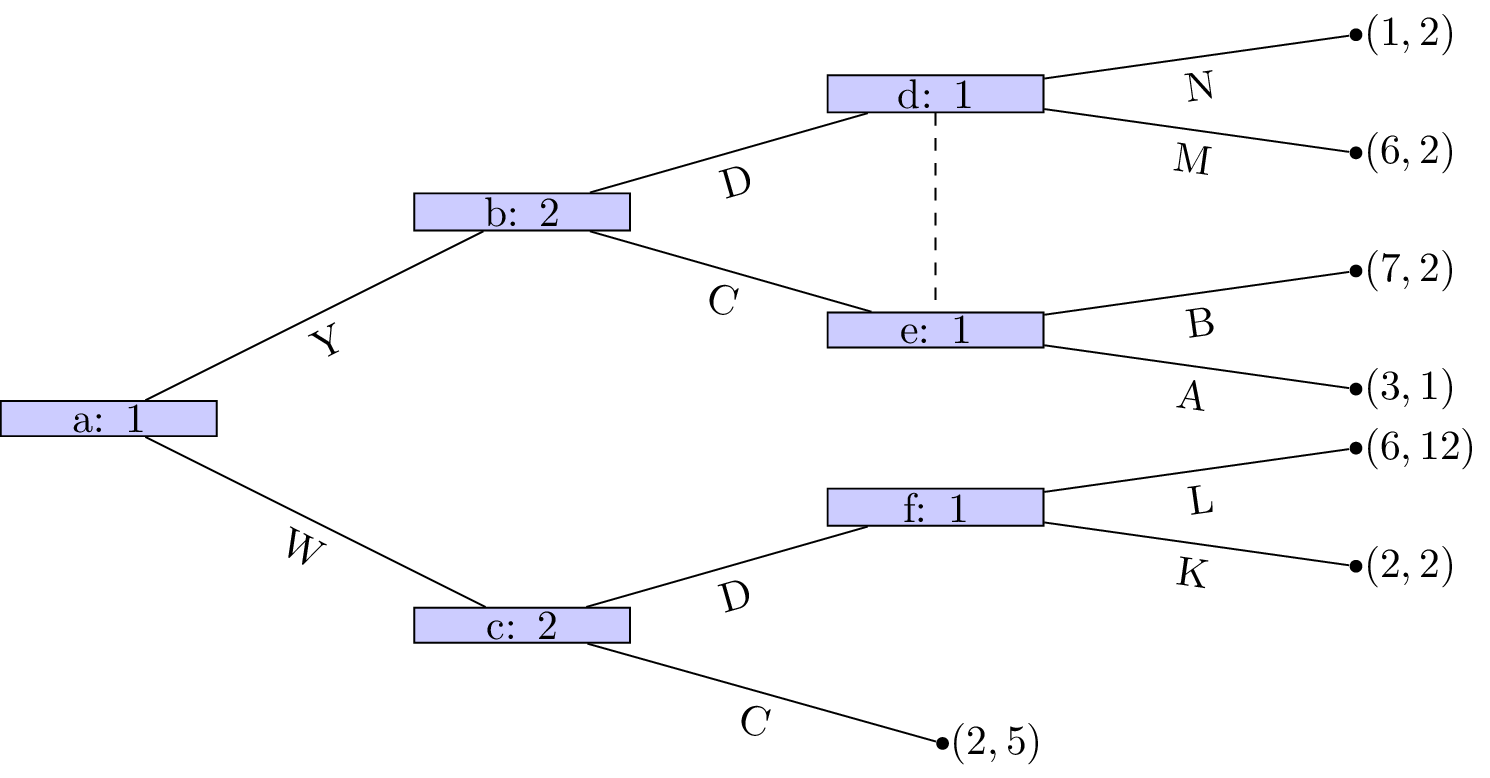
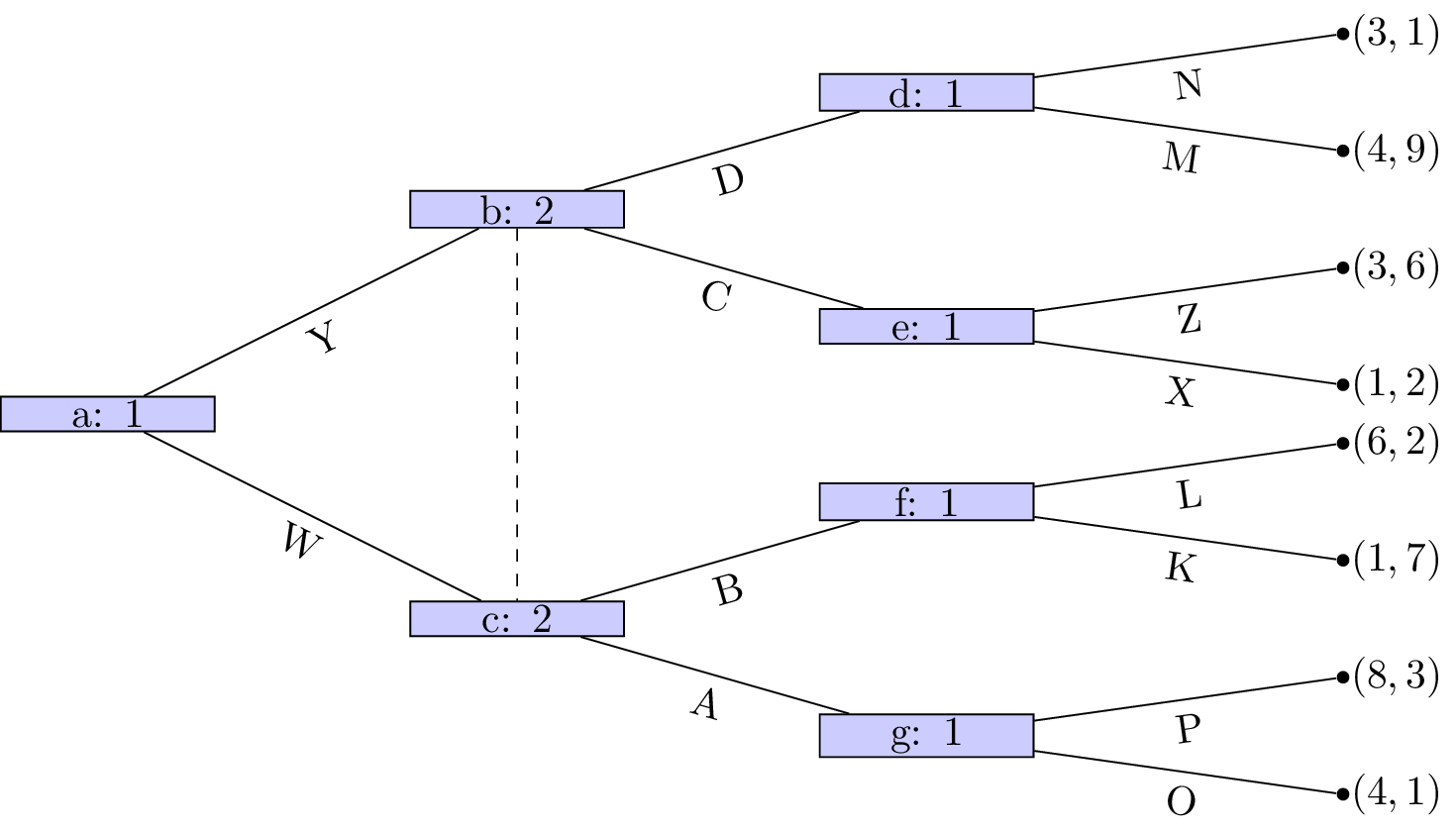
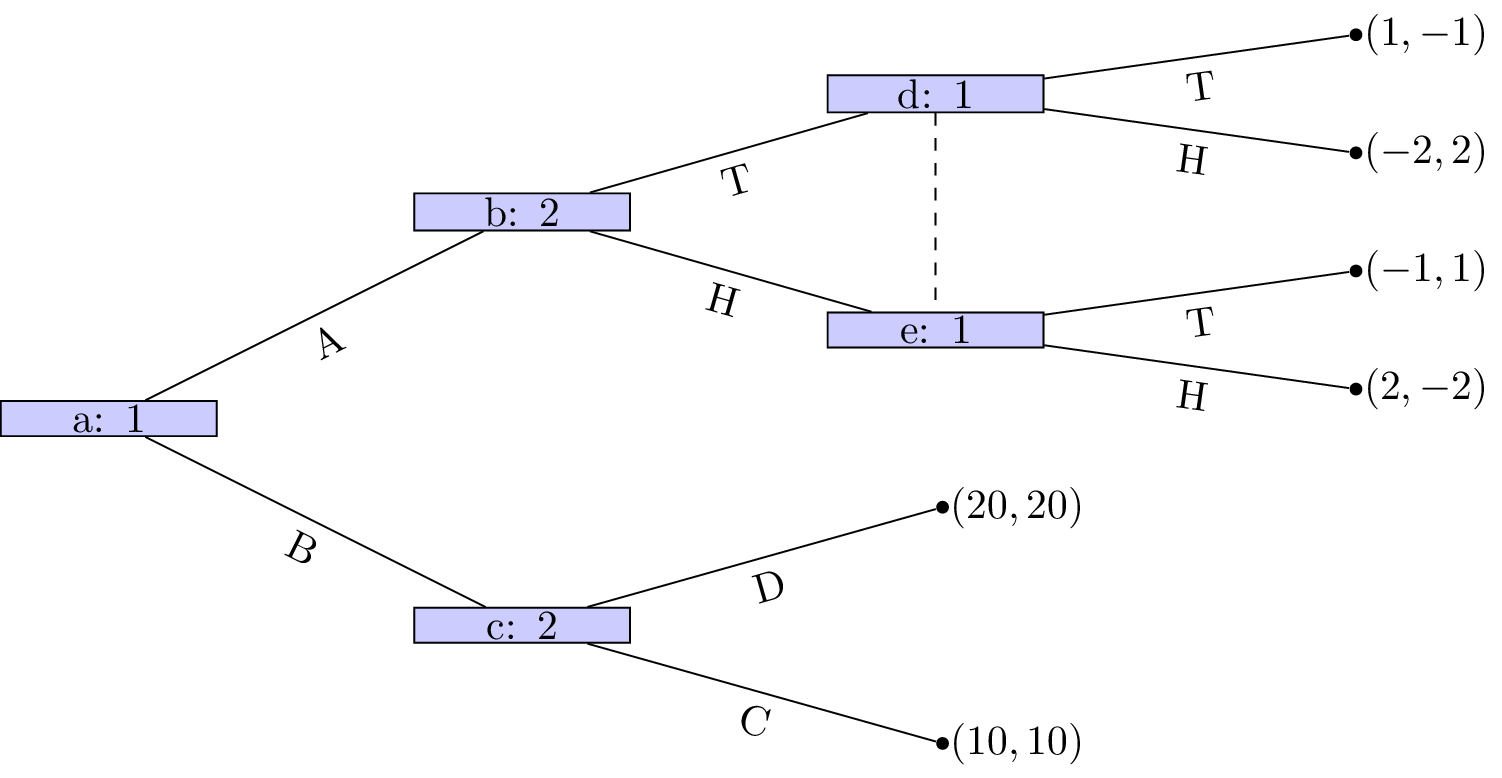
For the following stage games:
- Plot all possible utility pairs for \(T=2\);
- Recalling that subgame perfect equilibrium for the repeated game must play a stage Nash equilibrium in the final stage attempt to identify a subgame perfect Nash equilibrium for the repeated game that is not a sequence of stage Nash profiles.
\[\begin{pmatrix} (4,3)&(7,6)\\ (1,1)&(4,3) \end{pmatrix}\]
\[\begin{pmatrix} (5,4)&(0,3)\\ (0,3)&(1,4)\\ (3,6)&(0,3)\\ \end{pmatrix}\]
\[\begin{pmatrix} (1,2)&(0,3)&(-1,1)\\ (-1,0)&(-1,-1)&(0,1) \end{pmatrix}\]
Consider the following stage game:
\[\begin{pmatrix} (-1,1)&(3,-7)\\ (-2,6)&(2,2) \end{pmatrix}\]
- For \(\delta=1/3\) obtain the utilities for the infinitely repeated game for the strategies \(S_D\): "play the first strategy throughout" and \(S_C\): "play the second strategy throughout".
- Plot the space of feasible average payoffs and the space of individually rational payoffs.
- State whether or not it is possible according to the Folk theorem to obtain \(\delta\) that ensures that a strategy profile exists that would give a subgame perfect Nash equilibrium with average payoffs: \((3/2,3/2)\), \((0,3)\), \((2,6)\) and \((2,0)\).