Chapter 4 - Best responses

Recap

Predicting rational behaviour using dominated strategies;
The CKR;

We did discover certain games that did not have any dominated strategies.

Best response functions

Definition of a best response

In an $N$ player normal form game. A strategy $s^*$ for player $i$ is a best response to some strategy profile $s_{-i}$ if and only if $u_i(s^*,s_{-i})\geq u_{i}(s,s_{-i})$ for all $s\in S_i$.

We can now start to predict rational outcomes in pure strategies by identifying all best responses to a strategy.

$\begin{pmatrix} (1,3)&(4,2)&(2,2)\\ (4,0)&(0,3)&(4,1)\\ (2,5)&(3,4)&(5,6) \end{pmatrix}$

We will underline the best responses for each strategy giving ($r_i$ is underlined if it is a best response to $s_j$ and vice versa):

$\begin{pmatrix} (1,\underline{3})&(\underline{4},2)&(2,2)\\ (\underline{4},0)&(0,\underline{3})&(4,1)\\ (2,5)&(3,4)&(\underline{5},\underline{6}) \end{pmatrix}$

We see that $(r_3,c_3)$ represented a pair of best responses. What can we say about the long term behaviour of this game?

Best responses against mixed strategies

We can identify best responses against mixed strategies. Let us take a look at the matching pennies game:

$\begin{pmatrix} (1,-1)&(-1,1)\\ (-1,1)&(1,-1) \end{pmatrix}$

If we assume that player 2 plays a mixed strategy $\sigma_2=(x,1-x)$ we have:

$u_1(r_1,\sigma_2)=2x-1$

and

$u_1(r_2,\sigma_2)=1-2x$

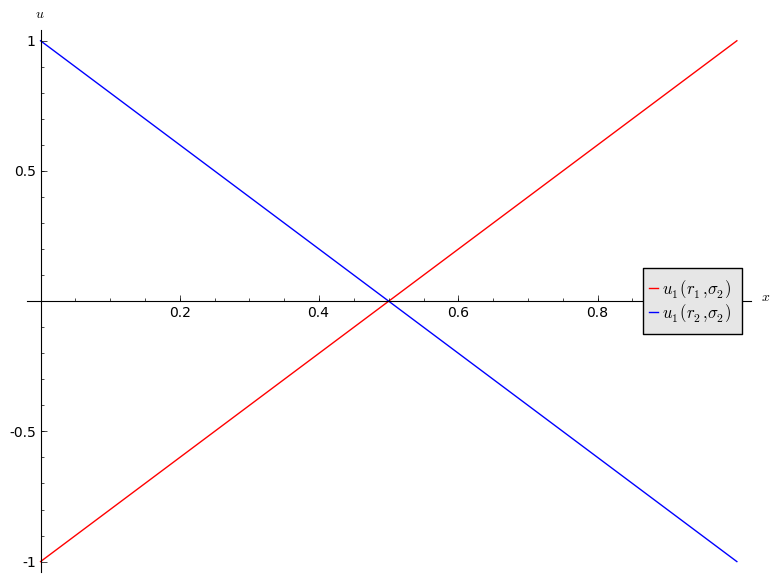
$Mixed strategies fox the matching pennies game. \label{L04-plot01}$

We see that:

If $x<1/2$ then $r_2$ is a best response for player 1.
If $x>1/2$ then $r_1$ is a best response for player 1.
If $x=1/2$ then player 1 is indifferent.

Let us repeat this exercise for the battle of the sexes game.

$\begin{pmatrix} (3,2)&(0,0)\\ (1,1)&(2,3) \end{pmatrix}$

If we assume that player 2 plays a mixed strategy $\sigma_2=(x,1-x)$ we have:

$u_1(r_1,\sigma_2)=3x$

and

$u_1(r_2,\sigma_2)=2-x$

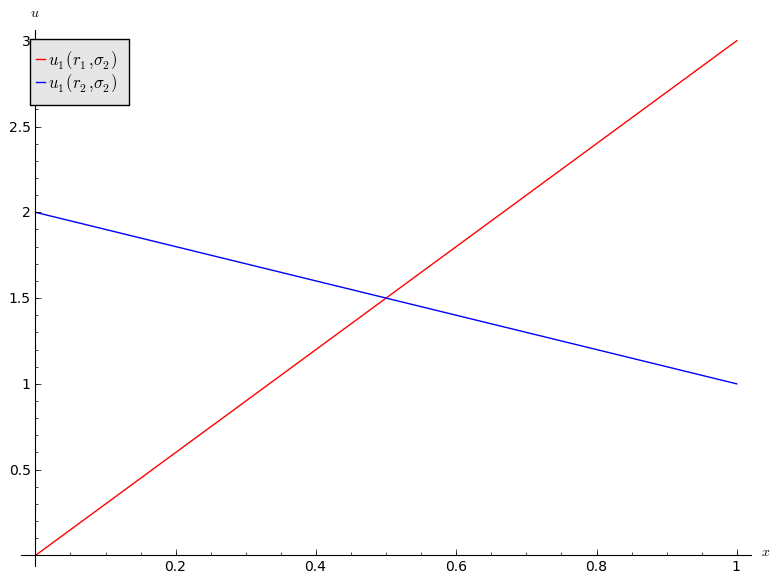
$Mixed strategies for the battle of the sexes game. \label{L04-plot02}$

We see that:

If $x<1/2$ then $r_2$ is a best response for player 1.
If $x>1/2$ then $r_1$ is a best response for player 1.
If $x=1/2$ then player 1 is indifferent.

Connection between best responses and dominance

Definition of the undominated strategy set

In an $N$ player normal form game, let us define the undominated strategy set $UD_i$:

$UD_i=\{s\in S_i\;|\; \text{s is not strictly dominated}\}$

If we consider the following game:

$\begin{pmatrix} (3,3)&(7,2)&(5,1)\\ (5,1)&(6,3)&(7,-1) \end{pmatrix}$

We have:

$UD_1=\{r_1,r_2\}$ $UD_2=\{c_1,c_2\}$

Definition of the best responses strategy set

In an $N$ player normal form game, let us define the best responses strategy set $B_i$:

$B_i=\{s\in S_i\;|\; \exists\;\sigma\in\Delta S_{-i}\text{ such that }s \text{ is a best response to }\sigma\}$

In other words $B_i$ is the set of functions that are best responses to some strategy profile in $S_{-i}$.

Let us try to identify $B_2$ for the above game. Let us assume that player 1 plays $\sigma_1=(x,1-x)$. This gives:

$u_2(\sigma_1,c_1)=1+2x$ $u_2(\sigma_1,c_2)=3-x$ $u_2(\sigma_1,c_3)=2x-1$

Plotted:

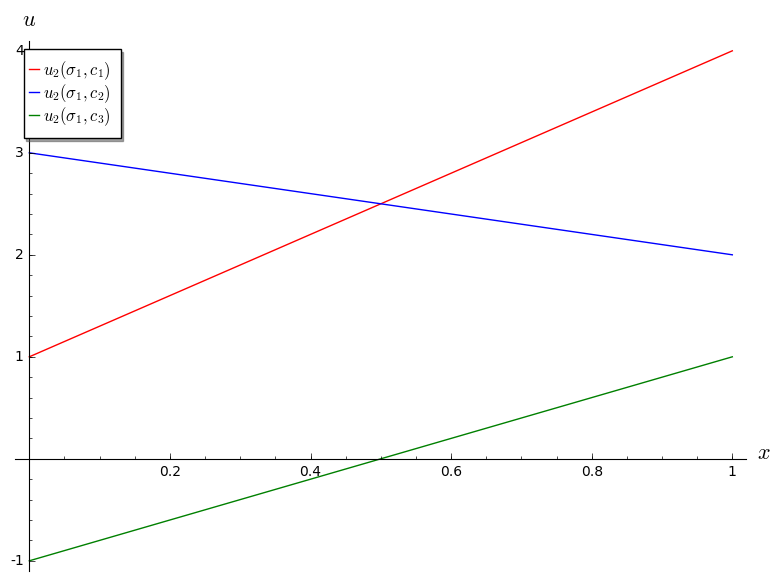
$Utilities of player 2 in our example. \label{L04-plot03}$

We see that $c_3$ is never a best response for player 2:

$B_2=\{c_1,c_2\}$

We will now attempt to identify $B_1$ for the above game. Let us assume that player two plays $\sigma_2=(x,y,1-x-y)$. This gives:

$u_1(r_1,\sigma_2)=xu_1(r_1,c_1)+yu_1(r_1,c_2)+(1-x-y)u_1(r_1,c_3)=3x+7y+5-5y-5x$ $u_1(r_2,\sigma_2)=xu_1(r_2,c_1)+yu_1(r_2,c_2)+(1-x-y)u_1(r_2,c_3)=5x+6y+7-7y-7x$

$u_1(r_1,\sigma_2)-u_1(r_2,\sigma_2)=3y - 2$

If we can find values of $y$ that give valid $\sigma_2=(x,y,1-x-y)$ and that make the above difference both positive and negative then:

$B_1=\{r_1,r_2\}$

$y=1$ gives $u_1(r_1,\sigma_2)-u_2(r_2,\sigma_2)=1>0$ (thus $r_1$ is best response to $\sigma_2=(0,1,0)$). Similarly, $y=0$ gives $u_1(r_1,\sigma_2)-u_2(r_2,\sigma_2)=-2<0$ (thus $r_2$ is best response to $\sigma_2=(x,0,1-x)$ for any $0\leq x \leq 1$) as required.

We have seen in our example that $B_i=UD_i$. This leads us to two Theorems (the proofs are omitted).

Theorem of equality in 2 player games

In a 2 player normal form game $B_i=UD_i$ for all $i\in{1,2}$.

This is however not always the case:

Theorem of inclusion in $N$ player games

In an $N$ player normal form game $B_i\subseteq UD_i$ for all $1 \leq i\leq n$.