#MAT013 Class Test

Instructions:

• This is an open book test. You are encouraged to use the internet, your notes etc…, however no communication with any other student is allowed.
• The output of this class test will be: a file containing the SAS program with any comments included and a file containing the R code with any comments included.

Once you have finished the test:

1. Call the file for the SAS code: SAS-lastname-STUDENTNUMBER (eg. SAS-Knight-123456) and call the file for the R code: R-lastname-STUDENTNUMBER (eg. R-Knight-123456).
2. Email both files to Joanna Emery ([email protected]) with ‘MAT013 - lastname-STUDENTNUMBER’ as the subject. ALL EMAILS MUST BE SENT BEFORE LEAVING THE COMPUTER LAB.

Class test:

1. Using both SAS and R (in other words attempt this question using SAS and then using R):

   Create a data set with two variables: “Week” and “Ranking”. For every week of the MAT013 course (1-5 including this class test) give a ranking of your enjoyment of each week of the course (1 being the best). Write some code (in both SAS and R) to sort this data set in descending order of the enjoyment ranking.

   [10]

2. Using SAS:

   The following directory: pairs.zip contains 20 pairs of data sets:

    A_1.csv, B_1.csv
    A_2.csv, B_2.csv
    A_3.csv, B_2.csv
    ...
    B_20.csv, B_20.csv
   

   For each pair write a new data file M_1.csv, M_2.csv, M_3.csv etc... which merges both files on the variable ID but ensuring that all entries from the B_*.csv file are included (even if they are missing from the A_*.csv file).

   [25]

3. Using R:

   A perfect number is a natural number that is equal to the sum of its divisors (excluding itself). For example \(1,2,4,7\) and \(14\) divide \(28\) and \(28=1+2+4+7+14\).

   Write code that writes to a csv file the first 10000 Natural numbers as well as a boolean variable indicating whether or not that number is perfect.

   [25]

4. Using either SAS or R, solve the following problem:

   The farmers’ union has asked all of the farmers to send in data sets with regards to the dimensions of their fields:

   • Each farmer can have multiple fields
   • The fields can be of various shapes as shown below:

   

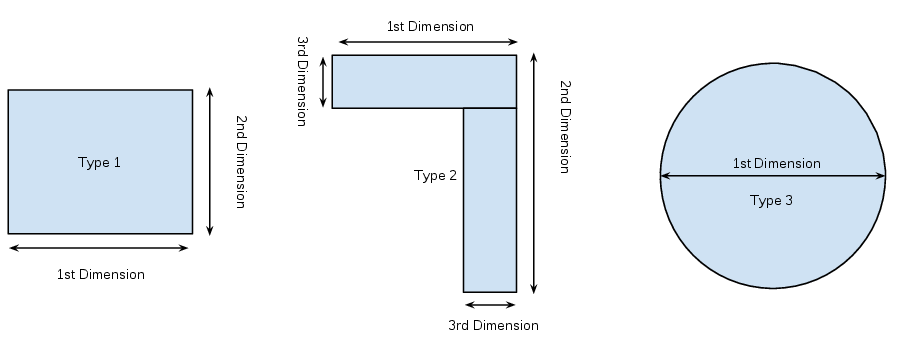
   • Each farmer might have made mistakes when filling in his data files.
   • If a dimension has value 0 it can be assumed that the particular field does not have that dimension.

   Answer the following questions:

   1. Using all the files available in Farmer_Fields.zip obtain the mean area of each field type. [15]
   2. What is the name of the Farmer with the biggest total field area? [5]
   3. What is the name of the Farmer with the smallest total field area? [5]
   4. Which farmer has the most fields? [5]
   5. Is there a correlation between number of fields and mean area of fields? [10]