Homework 5 Solution - Matching games, cooperative games and routing games

Obtain stable suitor optimal and reviewer optimal matchings for the matching games shown.
- Game 1:
  
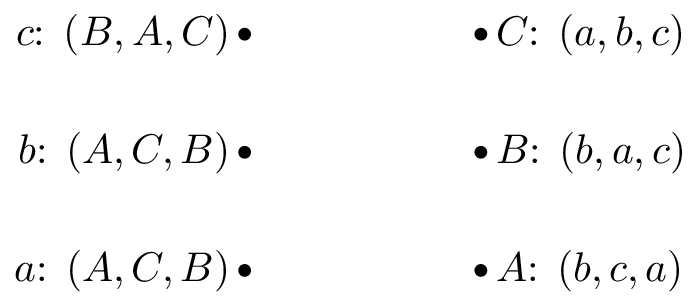
  $Matching game 1 \label{E05-img01}$
  
  Solution
  
  Following the algorithm:
  
  Suitor optimal: $\{a: C, b: A, c: B\}$ Reviewer optimal: $\{‘A’: ‘b’, ‘B’: ‘c’, ‘C’: ‘a’\}$
- Game 2:
  
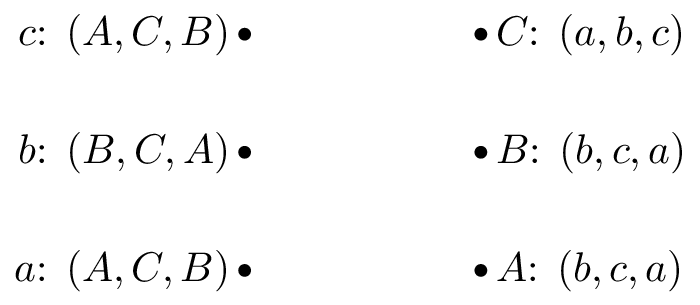
  $Matching game 2 \label{E05-img02}$
  
  Solution
  
  Following the algorithm:
  
  Suitor optimal: $\{a: C, b: B, c: A\}$ Reviewer optimal: $\{A: c, B: b, C: a\}$
- Game 3:
  
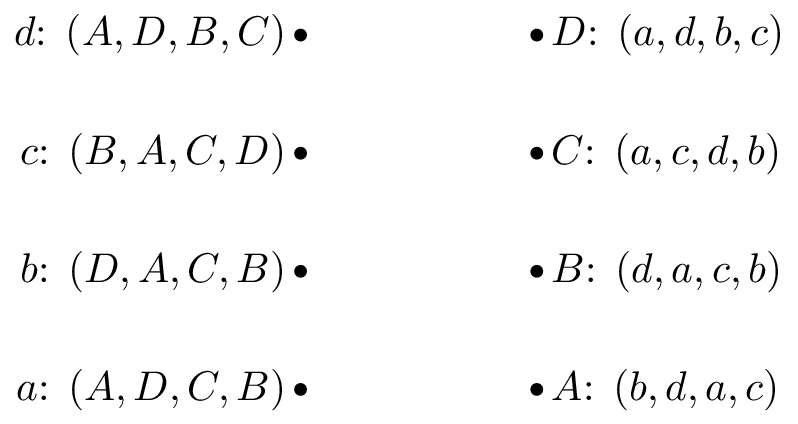
  $Matching game 3 \label{E05-img03}$
  
  Solution
  
  Following the algorithm:
  
  Suitor optimal: $\{a: D, b: A, c: C, d: B\}$ Reviewer optimal: $\{A: b, B: d, C: c, D: a\}$
- Game 4:
  
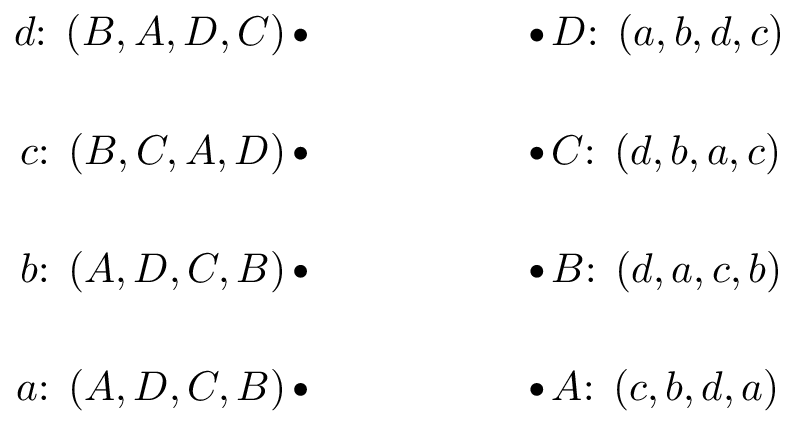
  $Matching game 4 \label{E05-img04}$
  
  Solution
  
  Following the algorithm:
  
  Suitor optimal: $\{a: D, b: A, c: C, d: B\}$ Reviewer optimal: $\{A: c, B: d, C: b, D: a\}$
Consider a matching game where all reviewers have the same preference list. Prove that there is a single stable matching.

Solution

Let $M$ be the suitor optimal matching (given by the Gale-Shapley algorithm).

Assume $\exists$ $M’\ne M$. As $M$ is reviewer sub-optimal $\exists$ a subset $\bar R\subseteq R$ such that: For all $r\in \bar R$: $M^{-1}(r)$ is worse than $M’^{-1}(r)$. For $r\in R\setminus \bar R$ $M^{-1}(r)=M’^{-1}(r)$.

Consider $\bar r\in\bar R$, as all reviewers have same reference list, let $\bar r$ be the reviewer with ‘‘best’’ suitor under matching $M$ (the matching given by the Gale Shapley algorithm).

When considering $M’$, reviewers outside of $\bar R$ have same matching as in $M$. All reviewers in $\bar R$ must have a ‘‘better’’ matching.

We have however assumed that $\bar r$ is the reviewer with the best matching in $\bar R$ thus $\bar r$ cannot be matched (it cannot improve) thus $M’$ is not a matching.
For the following cooperative games:

i. Verify if the game is monotonic. ii. Verify if the game is super additive. iii. Obtain the Shapley value.
$v_1(C)=\begin{cases} 5,&\text{if }C=\{1\}\\ 3,&\text{if }C=\{2\}\\ 2,&\text{if }C=\{3\}\\ 12,&\text{if }C=\{1,2\}\\ 5,&\text{if }C=\{1,3\}\\ 4,&\text{if }C=\{2,3\}\\ 13,&\text{if }C=\{1,2,3\}\\ \end{cases}$
Solution

Game is monotone but is not super additive: $v_1({1,3})=5$ and $v_1({1})+v_1({3})=5+2=7$.

The Shapley value is $\phi=(20/3, 31/6, 7/6)$.
$v_2(C)=\begin{cases} 6,&\text{if }C=\{1\}\\ 0,&\text{if }C=\{2\}\\ 5,&\text{if }C=\{1,2\}\\ \end{cases}$
Solution

Game is not monotone: $v_2({1})=6\geq v_2({1,2})=5$. Game is not super additive: $v_2({1,2})=5\leq v_2({1})+v_2({2})=6$.

The Shapley value is $\phi=(11/2,-1/2)$.
$v_3(C)=\begin{cases} 6,&\text{if }C=\{1\}\\ 6,&\text{if }C=\{2\}\\ 13,&\text{if }C=\{3\}\\ 6,&\text{if }C=\{1,2\}\\ 13,&\text{if }C=\{1,3\}\\ 13,&\text{if }C=\{2,3\}\\ 26,&\text{if }C=\{1,2,3\}\\ \end{cases}$
Game is monotone but not super additive: $v_3({1,2})=6\leq v_3({1})+v_3({2})=12$

The Shapley value is $\phi=(19/3, 19/3, 40/3)$.
$v_4(C)=\begin{cases} 6,&\text{if }C=\{1\}\\ 7,&\text{if }C=\{2\}\\ 0,&\text{if }C=\{3\}\\ 8,&\text{if }C=\{4\}\\ 7,&\text{if }C=\{1,2\}\\ 6,&\text{if }C=\{1,3\}\\ 12,&\text{if }C=\{1,4\}\\ 7,&\text{if }C=\{2,3\}\\ 12,&\text{if }C=\{2,4\}\\ 8&\text{if }C=\{3,4\}\\ 7,&\text{if }C=\{1,2,3\}\\ 24,&\text{if }C=\{1,2,4\}\\ 12,&\text{if }C=\{1,3,4\}\\ 12,&\text{if }C=\{2,3,4\}\\ 25,&\text{if }C=\{1,2,3,4\}\\ \end{cases}$
Game is monotone but not super additive: $v_4({1,2})=7\leq v_4({1})+v_4({2})=13$

The Shapley value is $\phi=(83/12, 89/12, 1/4, 125/12)$.
Prove that the Shapley value has the following properties:
- Efficiency
  
  Solution
  
  For every permutation $\pi$ we have:
  $\sum_{i=1}^{N}\Delta_{\pi}^{G}(i)=v(S_{\pi}(1)\cup \{1\})-v(S_{\pi}(1))+v(S_{\pi}(2)\cup \{2\})-v(S_{\pi}(2))\dots v(S_{\pi}(N)\cup N)-v(S_{\pi}(N))=v(S_{\pi}(N)\cup N)=v(N)$
  taking the mean over all permutations (which is by definition the Shapley value) we have the required result.
- Null player
  
  Solution
  
  Consider any permutation $\pi$ and a null player $i$. We have $v(S_{\pi}(i))\cup {i}=v(S_{\pi})$. Thus, $\Delta_{\pi}^{G}(i)=0$, as this holds for all $\pi$ the result follows.
- Symmetry
  
  Solution
  
  Assume that $i$ and $j$ are symmetric. Given a permutation $\pi$, let $\pi’$ denote the permutation obtained by swapping $i$ and $j$.
  - Assume that $i$ precedes $j$ in $\pi$, this gives $S_{\pi}(i)=S_{\pi’}(j)$, if we let $C=S_{\pi’}(j)$:
    $\Delta_{\pi}^{G}(i)=v(C\cup \{i\})-v(C)$
    and
    $\Delta_{\pi'}^{G}(j)=v(C\cup \{j\})-v(C)$
    By symmetry $\Delta_{\pi}^{G}(i)=\Delta_{\pi’}^{G}(j)$.
  - Assume that $i$ does not precede $j$ in $\pi$, let $C=S_{\pi}(i)\setminus {j}$. We have:
    $\Delta_{\pi}^{G}(i)=v(C\cup \{i\} \cup \{j\})-v(C\cup \{j\})$
    and
    $\Delta_{\pi'}^{G}(j)=v(C\cup \{j\} \cup \{i\})-v(C\cup \{i\})$
    Since $C\subseteq N$ and $i,j\notin C$ we have by symmetry $v(C\cup{i})=v(C\cup{j})$ and therefore $\Delta_{\pi}^{G}(i)=\Delta_{\pi’}^{G}(j)$.
  We have that $\Delta_{\pi}^{G}(i)=\Delta_{\pi’}^{G}(j)$ for all $\pi\in\Pi_N$, there is an obvious bijection between all $\pi$ and corresponding $\pi’$ thus:
  
  as required.
- Additivity
Solution

Let $v^+$ be the characteristic function of the game $G^1+G^2$. Following from the definition of additivity it is immediate to note that we have $\Delta^{+}_{\pi}(i)=\Delta^{v_1}_{\pi}(i)+\Delta^{v_2}_{\pi}(i)$. The result follows.

Note that this does not prove that the Shapley value is the only vector that has those properties (it in fact is though).
Calculate the Nash flow and the optimal flow for the following routing game:

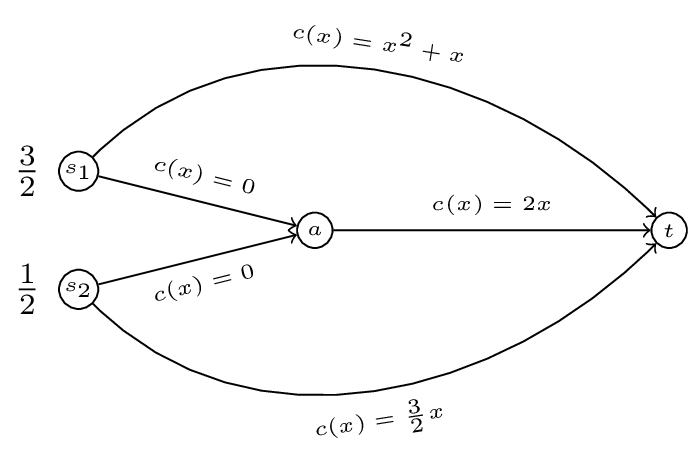
$Routing game 1\label{E05-img05}$

Solution

For the Nash flow:

Let $\alpha$ be the traffic along the top arc and $\beta$ the traffic along the bottom arc.

Assuming both commodities use both arcs available to them. By definition for commodity 1 we have:
$\alpha^2+\alpha=2(3/2-\alpha+1/2-\beta)$
By definition for commodity 2 we have:
$3/2\beta=2(3/2-\alpha+1/2-\beta)$
Solving this later equation gives:
$\beta=(8-4\alpha)/7$
Substituting this in to the first equation gives:
$\alpha^2+13/7\alpha-12/7=0$
which has solution $\alpha=\frac{1}{14} \, \sqrt{505} - \frac{13}{14}$, substituting this in to our expression for $\beta$ gives: $\beta = -2\frac{\sqrt{505}}{49} + \frac{82}{49}\approx .756$. This is not a feasible flow $\beta>1/2$, thus only 1 commodity will use the middle arc.

Let us assume commodity 1 uses the middle arc. We have:
$\alpha^2+\alpha=2(3/2-\alpha)$
which gives $\alpha=\frac{\sqrt{21}}{2}-3/2$. The corresponding cost to commodity 1 is $\approx 1.417$. Thus $\beta=1/2$ (for a cost to commodity 2 of $3/4$) is a Nash flow.

It can be proved (not in this course) that a Nash flow is unique but let us check. Let us assume commodity 2 uses the middle arc. We have:
$3/2\beta=2(1/2-\beta)$
which gives $\beta=2/7$. The corresponding cost to commodity 2 is $3/7$. The cost to commodity 1 (for $\alpha=3/2$) is $3.75$ so commodity 1 has an incentive to deviate to the middle arc.

For the Optimal flow we use the marginal costs:
$c^*(x) = (2x+1)x+x^2+x$ $c^*(x) = 4x$ $c^*(x) = 3x$
We now repeat the above:

By definition for commodity 1 we have:
${\left(2 \, \alpha + 1\right)} \alpha + \alpha^{2} + \alpha = 4(3/2-\alpha+1/2-\beta)$
By definition for commodity 2 we have:
$3\beta=4(3/2-\alpha+1/2-\beta)$
Solving this later equation gives:
$\beta=(8-4\alpha)/7$
Substituting this in to the first equation gives:
$(2\alpha + 1)\alpha + \alpha^2 + 19/7\alpha - 24/7 =0$
which has solution $\alpha=\frac{1}{21} \, \sqrt{673} - \frac{13}{21}$, substituting this in to our expression for $\beta$ gives: $\beta = \frac{-4\sqrt{673}}{147} + \frac{220}{147}\approx .791$. This is not a feasible flow $\beta>1/2$, thus only 1 commodity will use the middle arc.

Let us assume commodity 1 uses the middle arc. We have:
${\left(2 \, \alpha + 1\right)} \alpha + \alpha^{2} + \alpha = 4(3/2-\alpha)$
which gives $\alpha=\sqrt{3}-1$. The corresponding cost to commodity 1 is $\approx 3.071$. Thus $\beta=1/2$ (for a cost to commodity 2 of $3/2$) is a Nash flow.

Let us assume commodity 2 uses the middle arc. We have:
$3\beta=4(1/2-\beta)$
which gives $\beta=2/7$. The corresponding cost to commodity 2 is $6/7$.The cost to commodity 1 (for $\alpha=3/2$) is $9.75$ so commodity 1 has an incentive to deviate to the middle arc.
For a routing game the ‘Price of Anarchy’ is defined as:
$\text{PoA}=\frac{C(\tilde f)}{C(f^*)}$
For the game shown (a generalisation of “Pigou’s example”) obtain the PoA as a function of $\alpha$.

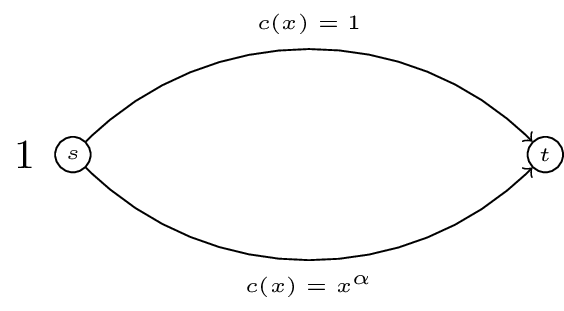
$A generalization of Pigou's example\label{E05-img07}$

Solution

Let $x$ be the flow along the bottom arc. The Nash flow $\tilde x$ is immediate:
$\tilde x=1$
giving $C(\tilde f)=1$

The optimal flow is $x^*$ solves:
$(\alpha+1)x^{\alpha}=1$
thus
$x^*=\left(\frac{1}{\alpha+1}\right)^{1/\alpha}$
giving
$C(f^*)=(1-x^*)+{x^*}^{\alpha}x^*=\left(\left(\frac{1}{\alpha+1}\right)^{1/\alpha}\right)^{\alpha}\left(\frac{1}{\alpha+1}\right)^{1/\alpha}+1-\left(\frac{1}{\alpha+1}\right)^{1/\alpha}$
Thus:
$\text{PoA}=\frac{1}{\left(\frac{1}{\alpha+1}\right)^{1+1/\alpha}+1-\left(\frac{1}{\alpha+1}\right)^{1/\alpha}}$
It can be shown that the above is a decreasing function in $\alpha$, this implies that as the ‘shortcut’ gets ‘better’ (recall that $x\leq 1$) the negative effect of selfish behaviour increases.