Chapter 16 - Cooperative games

Recap

We defined matching games;
We described the Gale-Shapley algorithm;
We proved certain results regarding the Gale-Shapley algorithm.

In this Chapter we’ll take a look at another type of game.

Cooperative Games

In cooperative game theory the interest lies with understanding how coalitions form in competitive situations.

Definition of a characteristic function game

A characteristic function game G is given by a pair $(N,v)$ where $N$ is the number of players and $v:2^{[N]}\to\mathbb{R}$ is a characteristic function which maps every coalition of players to a payoff.

Let us consider the following game:

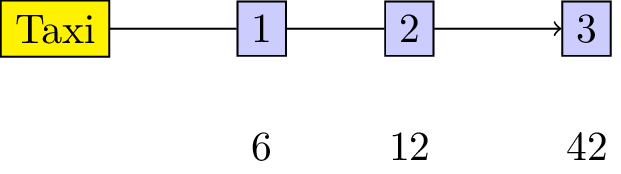
“3 players share a taxi. Here are the costs for each individual journey:

Player 1: 6

Player 2: 12

Player 3: 42 How much should each individual contribute?”

This is illustrated.

$A taxi journey. \label{L16-img01}$

To construct the characteristic function we first obtain the power set (ie all possible coalitions) $2^{{1,2,3}}=\{\emptyset,\{1\},\{2\},\{3\},\{1,2\},\{1,3\},\{2,3\},\Omega\}$ where $\Omega$ denotes the set of all players ($\{1,2,3\}$).

The characteristic function is given below:

$v(C)=\begin{cases} 6,&\text{if }C=\{1\}\\ 12,&\text{if }C=\{2\}\\ 42,&\text{if }C=\{3\}\\ 12,&\text{if }C=\{1,2\}\\ 42,&\text{if }C=\{1,3\}\\ 42,&\text{if }C=\{2,3\}\\ 42,&\text{if }C=\{1,2,3\}\\ \end{cases}$

Definition of a monotone characteristic function game

A characteristic function game $G=(N,v)$ is called monotone if it satisfies $v(C_2)\geq v(C_1)$ for all $C_1\subseteq C_2$.

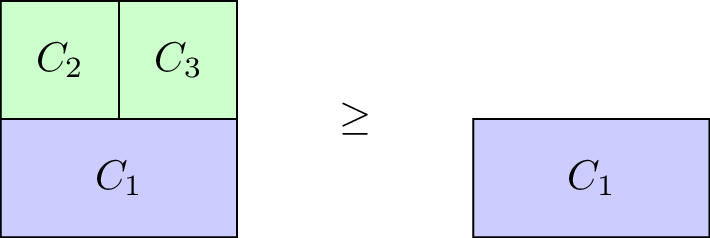
$A diagrammatic representation of monotonicity.\label{L16-img02}$

Our taxi example is monotone, however the $G=(3,v_1)$ with $v_1$ defined as:

$v_1(C)=\begin{cases} 6,&\text{if }C=\{1\}\\ 12,&\text{if }C=\{2\}\\ 42,&\text{if }C=\{3\}\\ 10,&\text{if }C=\{1,2\}\\ 42,&\text{if }C=\{1,3\}\\ 42,&\text{if }C=\{2,3\}\\ 42,&\text{if }C=\{1,2,3\}\\ \end{cases}$

is not.

Definition of a superadditive game

A characteristic function game $G=(N,v)$ is called superadditive if it satisfies $v(C_1\cup C_2)\geq v(C_1)+v(C_2).$ for all $C_1\cap C_2=\emptyset$.

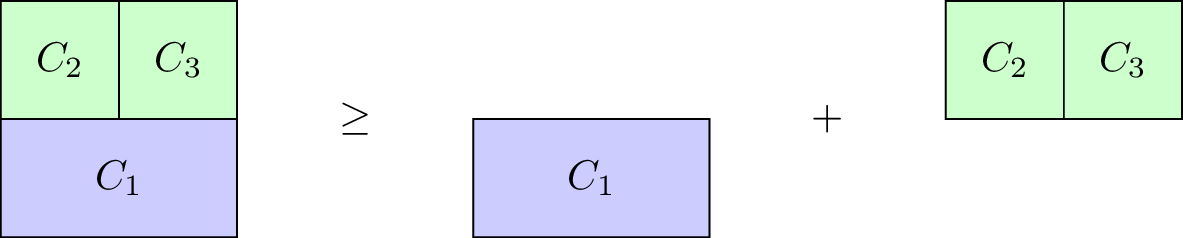
$A diagrammatic representation of superadditivity.\label{L16-img03}$

Our taxi example is not superadditive, however the $G=(3,v_2)$ with $v_2$ defined as:

$v_2(C)=\begin{cases} 6,&\text{if }C=\{1\}\\ 12,&\text{if }C=\{2\}\\ 42,&\text{if }C=\{3\}\\ 18,&\text{if }C=\{1,2\}\\ 48,&\text{if }C=\{1,3\}\\ 55,&\text{if }C=\{2,3\}\\ 80,&\text{if }C=\{1,2,3\}\\ \end{cases}$

is.

Shapley Value

When talking about a solution to a characteristic function game we imply a payoff vector $\lambda\in\mathbb{R}_{\geq 0}^{N}$ that divides the value of the grand coalition between the various players. Thus $\lambda$ must satisfy:

$\sum_{i=1}^N\lambda_i=v(\Omega)$

Thus one potential solution to our taxi example would be $\lambda=(14,14,14)$. Obviously this is not ideal for player 1 and/or 2: they actually pay more than they would have paid without sharing the taxi!

Another potential solution would be $\lambda=(6,6,30)$, however at this point sharing the taxi is of no benefit to player 1. Similarly $(0,12,30)$ would have no incentive for player 2.

To find a “fair” distribution of the grand coalition we must define what is meant by “fair”. We require four desirable properties:

Efficiency;
Null player;
Symmetry;
Additivity.

Definition of efficiency

For $G=(N,v)$ a payoff vector $\lambda$ is efficient if:

$\sum_{i=1}^N\lambda_i=v(\Omega)$

Definition of null players

For $G(N,v)$ a payoff vector possesses the null player property if $v(C\cup i)=v(C)$ for all $C\in 2^{\Omega}$ then:

$x_i=0$

Definition of symmetry

For $G(N,v)$ a payoff vector possesses the symmetry property if $v(C\cup i)=v(C\cup j)$ for all $C\in 2^{\Omega}\setminus\{i,j\}$ then:

$x_i=x_j$

Definition of additivity

For $G_1=(N,v_1)$ and $G_2=(N,v_2)$ and $G^+=(N,v^+)$ where $v^+(C)=v_1(C)+v_2(C)$ for any $C\in 2^{\Omega}$. A payoff vector possesses the additivity property if:

$x_i^{(G^+)}=x_i^{(G_1)}+x_i^{(G_2)}$

We will not prove in this course but in fact there is a single payoff vector that satisfies these four properties. To define it we need two last definitions.

Definition of predecessors

If we consider any permutation $\pi$ of $[N]$ then we denote by $S_\pi(i)$ the set of predecessors of $i$ in $\pi$:

$S_\pi(i)=\{j\in[N]\;|\;\pi(j)<\pi(i)\}$

For example for $\pi=(1,3,4,2)$ we have $S_\pi(4)=\{1,3\}$.

Definition of marginal contribution

If we consider any permutation $\pi$ of $[N]$ then the marginal contribution of player $i$ with respect to $\pi$ is given by:

$\Delta_\pi^G(i)=v(S_{\pi}(i)\cup i)-v(S_{\pi}(i))$

We can now define the Shapley value of any game $G=(N,v)$.

Definition of the Shapley value

Given $G=(N,v)$ the Shapley value of player $i$ is denoted by $\phi_i(G)$ and given by:

$\phi_i(G)=\frac{1}{N!}\sum_{\pi\in\Pi_n}\Delta_\pi^G(i)$

As an example here is the Shapley value calculation for our taxi sharing game:

For $\pi=(1,2,3)$:

$\begin{aligned} \Delta_{\pi}^G(1)&=6\\ \Delta_{\pi}^G(2)&=6\\ \Delta_{\pi}^G(3)&=30\\ \end{aligned}$

For $\pi=(1,3,2)$:

$\begin{aligned} \Delta_{\pi}^G(1)&=6\\ \Delta_{\pi}^G(2)&=0\\ \Delta_{\pi}^G(3)&=36\\ \end{aligned}$

For $\pi=(2,1,3)$:

$\begin{aligned} \Delta_{\pi}^G(1)&=0\\ \Delta_{\pi}^G(2)&=12\\ \Delta_{\pi}^G(3)&=30\\ \end{aligned}$

For $\pi=(2,3,1)$:

$\begin{aligned} \Delta_{\pi}^G(1)&=0\\ \Delta_{\pi}^G(2)&=12\\ \Delta_{\pi}^G(3)&=30\\ \end{aligned}$

For $\pi=(3,1,2)$:

$\begin{aligned} \Delta_{\pi}^G(1)&=0\\ \Delta_{\pi}^G(2)&=0\\ \Delta_{\pi}^G(3)&=42\\ \end{aligned}$

For $\pi=(3,2,1)$:

$\begin{aligned} \Delta_{\pi}^G(1)&=0\\ \Delta_{\pi}^G(2)&=0\\ \Delta_{\pi}^G(3)&=42\\ \end{aligned}$

Using this we obtain:

$\phi(G)=(2,5,35)$

Thus the fair way of sharing the taxi fare is for player 1 to pay 2, player 2 to pay 5 and player 3 to pay 35.