Chapter 6 - Nash equilibria in mixed strategies

Recap

The definition of Nash equilibria;
Identifying Nash equilibria in pure strategies;
Solving the duopoly game;

This brings us to a very important part of the course. We will now consider equilibria in mixed strategies.

Recall of expected utility calculation

In the matching pennies game discussed previously:

$\begin{pmatrix} (1,-1)&(-1,1)\\ (-1,1)&(1,-1) \end{pmatrix}$

Recalling Chapter 2 a strategy profile of $\sigma_1=(.2,.8)$ and $\sigma_2=(.6,.4)$ implies that player 1 plays heads with probability .2 and player 2 plays heads with probability .6.

We can extend the utility function which maps from the set of pure strategies to $\mathbb{R}$ using expected payoffs. For a two player game we have:

$u_{i}(\sigma_1,\sigma_2)=\sum_{r\in S_1,c\in S_2}\sigma_1(r)\sigma_2(c)u_{i}(r,c)$

Obtaining equilibria

Let us investigate the best response functions for the matching pennies game.

If we assume that player 2 plays a mixed strategy $\sigma_2=(y,1-y)$ we have:

$u_1(r_1,\sigma_2)=2y-1$ and $u_1(r_2,\sigma_2)=1-2y$

shown:

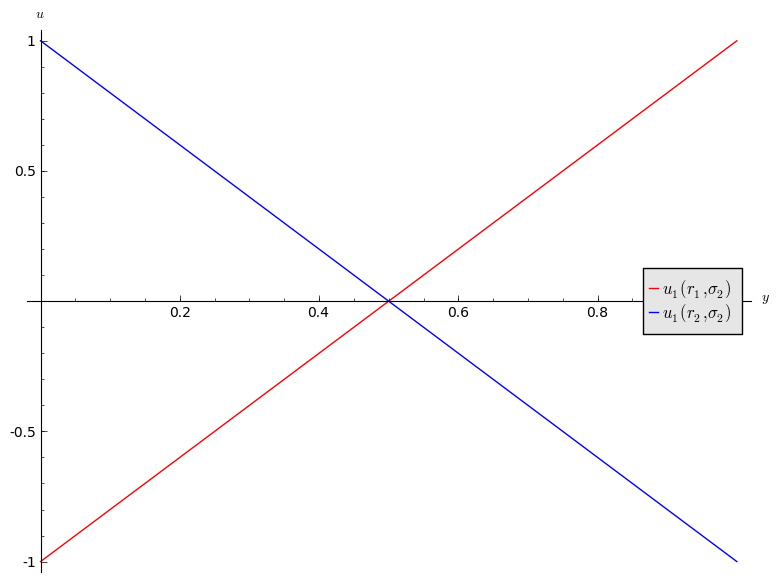
$Utilities of player 1 in the matching pennies game.\label{L06-plot01}$

If $y<1/2$ then $r_2$ is a best response for player 1.
If $y>1/2$ then $r_1$ is a best response for player 1.
If $y=1/2$ then player 1 is indifferent.

If we assume that player 1 plays a mixed strategy $\sigma_1=(x,1-x)$ we have:

$u_2(\sigma_1,c_1)=1-2x$ and $u_2(\sigma_1,c_2)=2x-1$

shown:

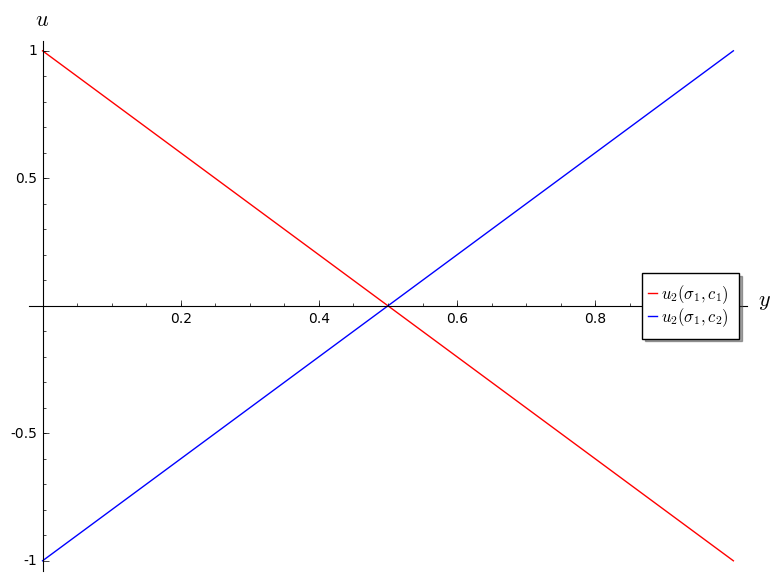
$Utilities of player 2 in the matching pennies game.\label{L06-plot02}$

Thus we have:

If $x<1/2$ then $c_1$ is a best response for player 2.
If $x>1/2$ then $c_2$ is a best response for player 2.
If $x=1/2$ then player 2 is indifferent.

Let us draw both best responses on a single diagram, indicating the best responses in each quadrant. The arrows show the deviation indicated by the best responses.

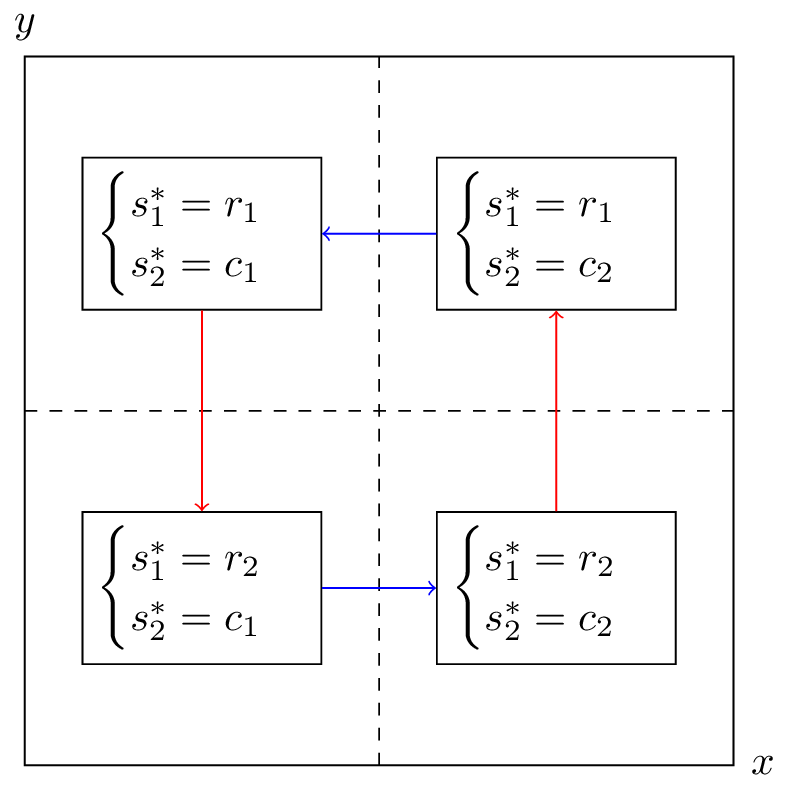
$Best response moves based on current strategy. \label{L06-img01}$

If either player plays a mixed strategy other than $(1/2,1/2)$ then the other player has an incentive to modify their strategy. Thus the Nash equilibria is:

$((1/2,1/2),(1/2,1/2))$

This notion of “indifference” is important and we will now prove an important theorem that will prove useful when calculating Nash Equilibria.

Equality of payoffs theorem

Definition of the support of a strategy

In an $N$ player normal form game the support of a strategy $\sigma\in\Delta S_i$ is defined as: $\mathcal{S}(\sigma)=\{s\in S_i\;|\;\sigma(s)>0\}$

I.e. the support of a strategy is the set of pure strategies that are played with non zero probability.

For example, if the strategy set is ${A,B,C}$ and $\sigma=(1/3,2/3,0)$ then $\mathcal{S}(\sigma)={A,B}$.

Theorem of equality of payoffs

In an $N$ player normal form game if the strategy profile $(\sigma_i,s_{-i})$ is a Nash equilibria then:

$u_{i}(\sigma_i,s_{-i})=u_{i}(s,s_{-i})\text{ for all }s\in\mathcal{S}(\sigma_i)\text{ for all }1\leq i\leq N$

Proof

If $|\mathcal{S}(\sigma_i)|=1$ then the proof is trivial.

We assume that $|\mathcal{S}(\sigma_i)|>1$. Let us assume that the theorem is not true so that there exists $\bar s\in\mathcal{S}(\sigma)$ such that

$u_{i}(\sigma_i,s_{-i})\ne u_{i}(\bar s,s_{-i})$

Without loss of generality let us assume that:

$\bar s=\text{argmax}_{s\in\mathcal{S}(\sigma)}u_i(s,s_{-i})$

Thus we have:

$\begin{aligned} u_i(\sigma_i,s_{-i})&=\sum_{s\in\mathcal{S}(\sigma_i)}\sigma_i(s)u(s,s_{-i})\\ &\leq \sum_{s\in\mathcal{S}(\sigma_i)}\sigma_i(s)u(\bar s,s_{-i})\\ &\leq u(\bar s,s_{-i})\sum_{s\in\mathcal{S}(\sigma_i)}\sigma_i(s)\\ &\leq u(\bar s,s_{-i})\\ \end{aligned}$

Giving:

$u_{i}(\sigma_i,s_{-i})< u_{i}(\bar s,s_{-i})$

which implies that $(\sigma_i,s_{-i})$ is not a Nash equilibrium.

Example

Let’s consider the matching pennies game yet again. To use the equality of payoffs theorem we identify the various supports we need to try out. As this is a $2\times 2$ game we can take $\sigma_1=(x,1-x)$ and $\sigma_2=(y,1-y)$ and assume that $(\sigma_1,\sigma_2)$ is a Nash equilibrium.

from the theorem we have that $u_1(\sigma_1,\sigma_2)=u_1(r_1,\sigma_2)=u_1(r_2,\sigma_2)$

$\begin{aligned} u_1(r_1,\sigma_2)&=u_1(r_2,\sigma_2)\\ y-(1-y)&=-y+(1-y)\\ y&=1/2 \end{aligned}$

Thus we have found player 2’s Nash equilibrium strategy by finding the strategy that makes player 1 indifferent. Similarly for player 1:

$\begin{aligned} u_2(\sigma_1,c_1)&=u_2(\sigma_1,c_2)\\ -x+(1-x)&=x-(1-x)\\ x&=1/2 \end{aligned}$

Thus the Nash equilibria is:

$((1/2,1/2),(1/2,1/2))$

To finish this chapter we state a famous result in game theory:

Nash’s Theorem

Every normal form game with a finite number of pure strategies for each player, has at least one Nash equilibrium.